 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Завдання для розрахунку. 1. Знайти наближення функції на інтервалі з використанням лінійного p1(x), квадратичного p2(x) та кубічного p3(x) поліномів лаґр
|
|
1. Знайти наближення функції 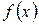 на інтервалі
на інтервалі  з використанням лінійного P 1(x), квадратичного P 2(x) та кубічного P 3(x) поліномів Лаґранжа. Для значень x, що розбивають інтервал
з використанням лінійного P 1(x), квадратичного P 2(x) та кубічного P 3(x) поліномів Лаґранжа. Для значень x, що розбивають інтервал  з кроком h, розрахувати значення функції
з кроком h, розрахувати значення функції 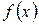 , поліномів Лаґранжа P 1(x), P 2(x), P 3(x) та зобразити розв’язок у табличному й графічному вигляді з використанням пакетів Mathcad та Matlab. Визначити помилки наближень. Порівняти результати наближення функції з точним розв’язком
, поліномів Лаґранжа P 1(x), P 2(x), P 3(x) та зобразити розв’язок у табличному й графічному вигляді з використанням пакетів Mathcad та Matlab. Визначити помилки наближень. Порівняти результати наближення функції з точним розв’язком 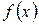 та проаналізувати точність поліномів Лаґранжа між собою. Необхідні дані взяти з табл. 4.3.
та проаналізувати точність поліномів Лаґранжа між собою. Необхідні дані взяти з табл. 4.3.
2. Побудувати таблицю різницевих відношень для функції  за точками xk,
за точками xk,  та знайти поліноми Ньютона P 1(x), P 2(x), P 3(x), P 4(x). Для значень x, що розбивають інтервал [a; b] з кроком h, розрахувати значення функції
та знайти поліноми Ньютона P 1(x), P 2(x), P 3(x), P 4(x). Для значень x, що розбивають інтервал [a; b] з кроком h, розрахувати значення функції 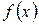 , поліномів Ньютона P 1(x), P 2(x), P 3(x), P 4(x) та зобразити розв’язок у табличному й графічному вигляді з використанням пакетів Mathcad та Matlab. Порівняти результати наближення функції з точним розв’язком
, поліномів Ньютона P 1(x), P 2(x), P 3(x), P 4(x) та зобразити розв’язок у табличному й графічному вигляді з використанням пакетів Mathcad та Matlab. Порівняти результати наближення функції з точним розв’язком 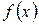 та проаналізувати точність поліномів Ньютона між собою. Необхідні дані взяти з табл. 4.3.
та проаналізувати точність поліномів Ньютона між собою. Необхідні дані взяти з табл. 4.3.
3. Знайти наближення Паде RN,M (x) для функції 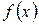 . Подати розв’язок у графічному вигляді з використанням пакетів Mathcad чи Matlab. Визначити помилку наближення. Необхідні дані взяти з табл. 4.4.
. Подати розв’язок у графічному вигляді з використанням пакетів Mathcad чи Matlab. Визначити помилку наближення. Необхідні дані взяти з табл. 4.4.
Таблиця 4.3 – Варіанти завдань для побудови наближуючих функцій
| № | Функція | Інтерполяційні поліноми | |||
| Лаґранжа | Ньютона | ||||
| P 1(x) | P 2(x) | P 3(x) | Pk (x), k= 1..4 | ||
 a =1; b =5; h =0.2
a =1; b =5; h =0.2
| 
| 
| 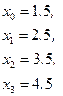
| 
|
Продовження таблиці 4.3
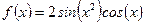 a =0; b =3; h =0.1
a =0; b =3; h =0.1
| 
| 
| 
| 
| |
 a =2; b =6; h =0.2
a =2; b =6; h =0.2
| 
| 
| 
| 
| |
 a = –1; b =3; h =0.1
a = –1; b =3; h =0.1
| 
| 
| 
| 
| |
 a =1; b =5; h =0.25
a =1; b =5; h =0.25
| 
| 
| 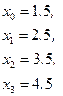
| 
| |
 a =0; b =5; h =0.2
a =0; b =5; h =0.2
| 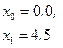
| 
| 
| 
| |
 a =1; b =3; h =0.1
a =1; b =3; h =0.1
| 
| 
| 
| 
| |
 a =-2; b =2; h =0.2
a =-2; b =2; h =0.2
| 
| 
| 
| 
|
Продовження таблиці 4.3
 a =0; b =4; h =0.1
a =0; b =4; h =0.1
| 
| 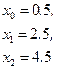
| 
| 
| |
 a =1; b =5; h =0.2
a =1; b =5; h =0.2
| 
| 
| 
| 
| |
 a =1; b =6; h =0.2
a =1; b =6; h =0.2
| 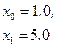
| 
| 
| 
| |
 a =-2; b =2; h =0.1
a =-2; b =2; h =0.1
| 
| 
| 
| 
| |
 a =0; b =4; h =0.1
a =0; b =4; h =0.1
| 
| 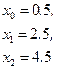
| 
| 
| |
 a =0; b =3; h =0.1
a =0; b =3; h =0.1
| 
| 
| 
| 
| |
 a = –1; b =3; h =0.1
a = –1; b =3; h =0.1
| 
| 
| 
| 
|
Продовження таблиці 4.3
 a =1; b =5; h =0.2
a =1; b =5; h =0.2
| 
| 
| 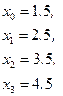
| 
| ||
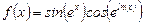 a =1; b =5; h =0.2
a =1; b =5; h =0.2
| 
| 
| 
| 
| ||
 a =1; b =3; h =0.1
a =1; b =3; h =0.1
| 
| 
| 
| 
| ||
 a =1; b =5; h =0.2
a =1; b =5; h =0.2
| 
| 
| 
| 
| ||
 a =-2; b =2; h =0.2
a =-2; b =2; h =0.2
| 
| 
| 
| 
| ||
 a =0; b =5; h =0.2
a =0; b =5; h =0.2
| 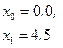
| 
| 
| 
| ||
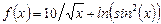 a =1; b =3; h =0.1
a =1; b =3; h =0.1
| 
| 
| 
| 
| ||
Продовження таблиці 4.3
 a =2; b =6; h =0.2
a =2; b =6; h =0.2
| 
| 
| 
| 
| ||||||
 a =1; b =3; h =0.1
a =1; b =3; h =0.1
| 
| 
| 
| 
| ||||||
 a =1; b =6; h =0.25
a =1; b =6; h =0.25
| 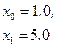
| 
| 
| 
| ||||||
Таблиця 4.4 – Варіанти завдань для побудови наближення Паде
| № | Функція f (x) | Наближення Паде | № | Функція f (x) | Наближення Паде |
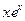
| R 3, 3(x) | 
| R 3, 2(x) | ||

| R 3, 2(x) | 
| R 3, 3(x) | ||

| R 2, 2(x) | 
| R 3, 2(x) | ||

| R 2, 1(x) | 
| R 4, 2(x) | ||

| R 3, 2(x) | 
| R 3, 3(x) | ||

| R 4, 2(x) | 
| R 2, 1(x) | ||

| R 3, 1(x) | 
| R 3, 2(x) | ||

| R 3, 3(x) | 
| R 4, 2(x) | ||

| R 3, 2(x) | 
| R 3, 3(x) | ||

| R 4, 2(x) | 
| R 3, 1(x) | ||
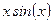
| R 2, 1(x) | 
| R 3, 2(x) | ||

| R 3, 3(x) | 
| R 3, 3(x) | ||

| R 4, 2(x) |
Продовження таблиці 4.4
| Відомі розклади Маклорена |





|
Дата публикования: 2015-11-01; Прочитано: 356 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
