 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Наближення Лаґранжа
|
|
Інтерполяція за допомогою цього методу полягає в обчисленні невідомих значень функції шляхом одержання зваженого середнього значення функції у відомих сусідніх точках [8].
При лінійній інтерполяції використовується відрізок прямої, що проходить через дві задані точки 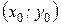 ,
, 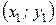 і записується у вигляді:
і записується у вигляді:
 , (4.3)
, (4.3)
де 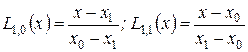 – коефіцієнти полінома Лаґранжа, який побудований на вузлах
– коефіцієнти полінома Лаґранжа, який побудований на вузлах 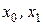 відповідно.
відповідно.
Вираз (4.3) можна записати у вигляді суми:
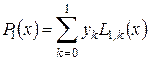 . (4.4)
. (4.4)
Якщо 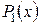 використовується для наближення
використовується для наближення 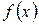 на інтервалі
на інтервалі 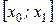 , такий процес називається інтерполяцією. Якщо
, такий процес називається інтерполяцією. Якщо 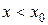 (або
(або 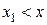 ), то використання
), то використання 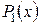 називають екстраполяцією.
називають екстраполяцією.
Загальний вид полінома Лаґранжа 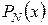 ступеня
ступеня 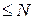 , що проходить через N +1 точку
, що проходить через N +1 точку  :
:
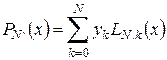 , (4.5)
, (4.5)
де  – коефіцієнти полінома Лагранжа.
– коефіцієнти полінома Лагранжа.
Коефіцієнти полінома Лаґранжа 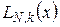 при фіксованому k мають властивості:
при фіксованому k мають властивості:
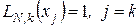 ; (4.6)
; (4.6)
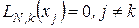 . (4.7)
. (4.7)
З (4.5) одержимо форму квадратичного й кубічного поліномів.
Квадратичний інтерполяційний поліном Лаґранжа побудований за трьома точками 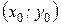 ,
, 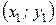 ,
, 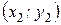 :
:
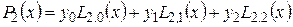 , (4.8)
, (4.8)
де 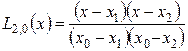 ;
; 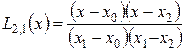 ;
; 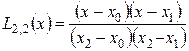 .
.
Кубічний інтерполяційний поліном Лаґранжа побудований за чотирма точками 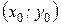 ,
, 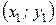 ,
, 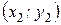 ,
, 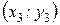 :
:
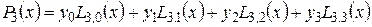 , (4.9)
, (4.9)
де 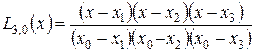 ;
; 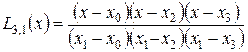 ;
;
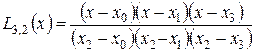 ;
; 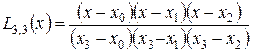 .
.
Дата публикования: 2015-11-01; Прочитано: 317 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
