Геометрическое изображение вещественных чисел

Рассмотрим произвольную прямую. На ней можно указать два противоположных направления. Выберем одно из направлений и масштабную единицу для измерения длин отрезков.

Определение. Прямая с выбранным на ней направлением называется осью.

Рассмотрим на оси две произвольные точки А и В.

Определение. Отрезок с граничными точками А и В называется направленным, если указано, какая из этих точек считается началом, а какая – концом отрезка.

Направленный отрезок с началом в точке А и концом в точке В обозначим 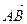и будем считать, что он направлен от начала отрезка к концу. Нулевыми направленными отрезками будем называть те, у которых начало и конец совпадают. Длина направленного отрезка 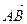обозначается 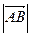или .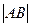

Для направленных отрезков, лежащих на оси (или на параллельных осях), вводится понятие величины направленного отрезка.

Определение. Величиной АВ направленного отрезка 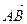называется число, равное 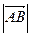, если направления отрезка и оси совпадают, и 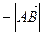, если эти направления противоположны.

Величины направленных отрезков 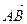и 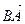при любом направлении оси отличаются знаками.

Если точки А и В совпадают, то величина направленного отрезка 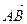считается равной нулю.

Определение. Два ненулевых направленных отрезка называются равными, если при совмещении начал этих отрезков совпадают и их концы. Любые два нулевых направленных отрезка считаются равными.

Над направленными отрезками определены следующие операции - операция сложения и умножения на число.

D

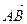Определение. Суммой направленных отрезков и 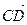называется направленный отрезок 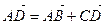, полученный при совмещении начала 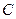отрезка 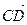с концом 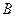отрезка .

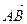Теорема. Величина суммы направленных отрезков равна сумме величин слагаемых отрезков.

Доказательство. Пусть хотя бы один из отрезков 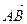и 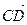является нулевым, то в этом случае сумма совпадает с другим отрезком и утверждение теоремы справедливо. Если оба отрезка ненулевые, то при совмещении начала 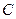отрезка 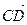с концом 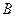отрезка 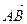получим, что 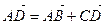. Рассмотрим случай, когда оба отрезка 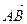и 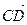направлены в одну сторону. В этом случае длина отрезка 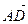равна сумме длин отрезков 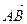и 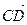, причем направление 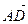совпадает с направлением каждого из отрезков 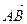и 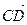. Поэтому справедливо равенство 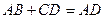. 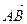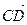Рассмотрим случай, когда отрезки и направлены в противоположные стороны. В этом случае величины отрезков 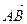и 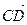имеют разные знаки, поэтому 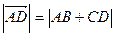. Направление отрезка 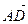совпадает с направлением наибольшего по длине из отрезков 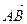и 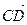, следовательно, знак величины отрезка 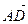совпадает со знаком числа 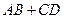, т. е. справедливо равенство 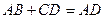. Теорема доказана.

Основное тождество. Для любых трех точек А, В, С, расположенных на оси, величины направленных отрезков 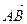, 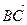и 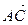удовлетворяют соотношению .

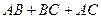Это тождество следует из доказанной выше теоремы.

Определение. Произведением направленного отрезка 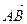на число a называется направленный отрезок, обозначаемый 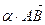, длина которого равна произведению числа 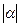на длину отрезка 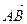и направление которого совпадает с направлением отрезка 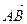при 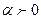и противоположно направлению 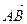при .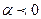

Рассмотрим произвольную прямую, на которой выбрано направление и некоторая точка О, называемая началом координат.

Определение. Прямая с выбранным направлением, масштабной единицей и началом координат называется координатной осью.

Пусть М – произвольная точка на выбранной прямой.

Точке М поставим в соответствие число х, равное величине ОМ направленного отрезка 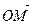. Число х называется координатой точки М.

Таким образом, каждой точке координатной прямой соответствует определенное вещественное число – ее координата. Верно и обратное утверждение: любому вещественному числу х соответствует некоторая точка М на координатной прямой, координата которой равна х. Следовательно, вещественные числа можно изображать точками на координатной прямой. Поэтому около точки на координатной прямой часто указывают число – ее координату.

		О		х

Пусть точка М₁ имеет координату х₁, а точка М₂ – координату х₂.

Выразим величину М₁М₂ направленного отрезка 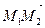через координаты точек М₁ и М₂. Согласно основному тождеству ОМ₁ + М₁М₂ = ОМ₂. Тогда М₁М₂ = ОМ₂ - ОМ₁, но ОМ₁ = х₁, ОМ₂ = х₂, поэтому М₁М₂ = х₂ – х₁.