 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Множества. Обозначения. Логические символы
|
|
ВЕЩЕСТВЕННЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА
Множества. Обозначения. Логические символы
Понятие множества является одним из основных в математике. Слова «совокупность», «семейство», «система», «набор» и т. д. – синонимы слова «множество». Множество может содержать конечное (количество студентов в аудитории) или бесконечное (количество точек на прямой) число произвольных объектов.
Определение. Объекты, из которых состоит множество, называютсяего элементами, или точками.
Множества часто обозначают большими буквами, а его элементы – маленькими. Если 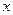 – элемент множества
– элемент множества 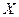 , то пишут
, то пишут 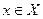 , в противном случае ─
, в противном случае ─  . Если
. Если 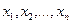 - некоторые элементы множества
- некоторые элементы множества 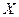 , то запись
, то запись 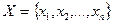 означает, что множество
означает, что множество 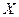 состоит из элементов
состоит из элементов 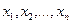 .
.
Пусть даны два множества 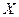 и
и 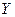 . Если
. Если 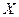 и
и 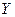 состоят из одних и тех же элементов, то говорят, что эти множества совпадают, и пишут
состоят из одних и тех же элементов, то говорят, что эти множества совпадают, и пишут 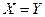 . Если в
. Если в 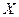 нет элементов, не принадлежащих
нет элементов, не принадлежащих 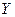 , то
, то 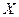 содержится в
содержится в 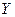 (
(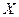 – подмножество множества
– подмножество множества 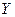 ). В этом случае пишут
). В этом случае пишут 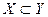 , или
, или 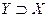 (
(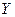 содержит
содержит 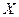 ). Если
). Если 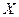 не содержится в
не содержится в 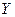 , то пишут
, то пишут 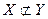 .
.
В математике часто используется пустое множество. Оно не содержит ни одного элемента и обозначается символом Æ. Пустое множество является подмножеством любого множества.
В математических предложениях повторяются отдельные слова и целые выражения. Поэтому для их записи используется логическая символика.
Рассмотрим несколько самых простых и наиболее употребляемых логических символов. Вместо слова «существует» или «найдется» используют символ $ (перевернутая латинская буква Е от английского слова Existence – «существование»), а вместо слов «любой», «каждый», «всякий» ─ символ " (перевернутое латинское А от английского слова Any ─ любой).
Например, запись 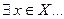 означает, что «существует элемент
означает, что «существует элемент 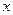 из множества
из множества 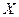 …». Запись
…». Запись 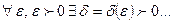 означает: «для любого
означает: «для любого 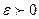 найдется
найдется 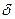 , зависящее от
, зависящее от 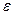 и большее 0…».
и большее 0…».
Для облегчения понимания и чтения утверждений, записанных с помощью логических символов, все, что относится только к каждому из них, заключается в круглые скобки. Например, запись

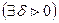
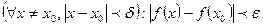
читается так: «для любого 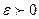 существует
существует 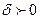 такое, что для всех
такое, что для всех 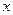 , не равных
, не равных 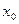 и удовлетворяющих неравенству
и удовлетворяющих неравенству 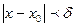 , выполняется неравенство
, выполняется неравенство  .
.
Дата публикования: 2015-11-01; Прочитано: 702 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
