Индивидуальное задание № 25

Найдите уравнения прямолинейных образующих поверхности второго порядка Ф, проходящих через точку М Î Ф, если:

1. Ф: , M (-5; 2; -1).

2. Ф: 9 x ² – y ² – 6 z = 0, M (-2; 0; 6).

3. Ф: x ² + 25 y ² – z ² - 1 = 0, M (3; ; -3).

4. Ф: x – y ² + 25 z ² = 0, M (0; 5; 1).

5. Ф: 36 x ² + y ² – 4 z ² - 4 = 0, M (1; 2; -3).

6. Ф: -2 x + y ² - 4 z ² = 0, M (0; 8; - 4).

7. Ф: 4 x ² - y ² + z ² - 4 = 0, M (-2; 4; 2).

8. Ф: x ² - 2 y – 25 z ² = 0, M (5; 0; 1).

9. Ф: x ² + y ² – 25 z ² - 25 = 0, M (3; - 4; 0).

10. Ф: x ² - 4 y – 4 z ² = 0, M (-2; 1; 0).

11. Ф: x ² + y ² – 9 z ² - 9 = 0, M (-3; 3; 1).

12. Ф: 2 x + 9 y ² - z ² = 0, M (8; 1; 5).

13. Ф: x ² - y ² + 4 z ² - 9 = 0, M (3; 4; -2).

14. Ф: 4 x ² - 2 y – z ² = 0, M (-1; -6; 4).

15. Ф: 25 x ² + y ² – z ² - 9 = 0, M (1; 0; - 4).

16. Ф: 9 x ² – 9 y ² + z = 0, M (3; -3; 0).

17. Ф: x ² - y ² + 25 z ² - 9 = 0, M (0; - 4; 1).

18. Ф: 4 x ² + y – z ² = 0, M (1; 5; 3).

19. Ф: , M (1; -3; 2).

20. Ф: , M (-2; 1; 3).

21. Ф: , M (4; -3; 0).

22. Ф: , M (5; ; 0).

23. Ф: x ² - 25 y ² - 9 z ² = -1, M (2 ; 0; 1).

24. Ф: 2 x – y ² + z ² = 0, M (0; 1; -1).

25. Ф: 4 x ² - y ² - z ² + 9 = 0, M (1; 2; 3).

26. Ф: 4 x ² - y ² + z = 0, M (3; 6; 0).

27. Ф: x ² + 25 y ² - z ² - 9 = 0, M (0; 1; 4).

28. Ф: x ² - y ² - 16 z = 0, M (5; -3; 1).

29. Ф: 9 x ² - 9 y ² + z ² – 9 = 0, M (; 0; 1).

30. Ф: x ² - y ² - 2 z = 0, M (2; 0; 2).

Вариант 31

Ф: 2 x ² - 5 y – 4 z ² = 0, M (; 0; 1).

Решение. Преобразуем уравнение поверхности Ф так, чтобы в левой и правой частях стояли произведения: 2 x ² – 4 z ² = 5 y; . Тогда первое семейство прямолинейных образующих задается системой: где a₁, b₁ – действительные числа, не равные нулю одновременно.

Второе семейство прямолинейных образующих задается системой: где a₂, b₂ – действительные числа, не равные нулю одновременно.

Найдем уравнение прямолинейной образующей из первого семейства, проходящей через точку М. Для этого подставим сначала координаты точки М в уравнения системы I:

Подставим найденное значение b₁ в уравнения системы I:

I:

Заметим, что a₁¹0 (если бы a₁ = 0, то a₁ и b₁ были бы равны 0 одновременно). Разделим обе части этих уравнений на a₁:

Получили уравнение искомой прямолинейной образующей первого семейства:

Найдем уравнение прямолинейной образующей из второго семейства, проходящей через точку М.

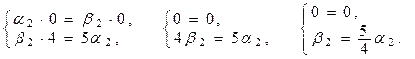
Заметим, что a₂ ¹ 0 (если бы a₂ = 0, то b₂ = 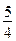× 0 = 0). Разделим обе части этих уравнений на a₂:

Получили уравнение искомой прямолинейной образующей второго семейства:

Ответ: и

Рекомендуемая литература

Основная

1. Атанасян Л.С., Базылев В.Т. Геометрия. В 2-х частях. Часть 1. – М.: Просвещение, 1986.

2. Атанасян Л.С. Геометрия. Часть 1. – М.: Просвещение, 1973.

3. Атанасян Л.С., Атанасян В.А. Сборник задач по геометрии. Часть 1. – М.: Просвещение, 1973.

4. Базылев В.Т., Дуничев К.И., Иваницкая В.П. Геометрия. Часть 1. – М.: Просвещение, 1974.

5. Базылев В.Т. и др. Сборник задач по геометрии. – М.: Просвещение, 1980.

6. Методические рекомендации по подготовке к практическим занятиям по курсу "Геометрия". Часть 1. Аналитическая геометрия. – Глазов, 1995.

7. Методические рекомендации по подготовке к практическим занятиям по курсу "Геометрия". Часть 2. Аналитическая геометрия. – Глазов, 1995.

Дополнительная

1. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1979.

2. Баврин И.И., Матросов В.Л. Общий курс высшей математики. – М.: Просвещение, 1995.

3. Беклемишев Д.В Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1979.

4. Беклемишева Л.А. и др. Сборник задач по аналитической геометрии и линейной алгебре. – М.: Наука, 1987.

5. Дадаян А.А., Масалова Е.С. Аналитическая геометрия и элементы линейной алгебры. – Минск: Вышэйшая школа, 1981.

6. Дадаян А.А., Масалова Е.С. Сборник задач по аналитической геометрии и элементам линейной алгебры. – Минск: Вышэйшая школа, 1982.

7. Данко П.Е. и др. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 1980.

8. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1980.

9. Судибор Г.П. Элементы аналитической геометрии и геометрических преобразований. – Минск: Вышэйшая школа, 1981.

10. Цубербиллер Ф.Н. Задачи и упражнения по аналитической геометрии. – М.: Наука, 1970.