 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Индивидуальное задание № 18
|
|
Найдите каноническое уравнение гиперболы и изобразите эту гиперболу, ее фокусы, асимптоты и директрисы, если известно, что:
1. Фокальное расстояние равно 
, уравнения асимптот l1 : у = 
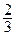х, l2 : у = - 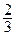х, Оу – мнимая ось симметрии.
2. Мнимая пол у ось равна 4, уравнения директрис d1: х - 
, d2: х + 
.
3. Гипербола проходит через точку М (
; -2), эксцентриситет равен 
; О у – мнимая ось симметрии.
4. Фокальное расстояние равно 
, уравнения асимптот: l1 : у = 
х, l2 : у = - х, Оу – мнимая ось симметрии.
5. Мнимая полуось равна 5 , уравнения директрис d1: х -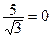 
, d2: х + .
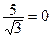6. Гипербола проходит через точку М (3 ; 2), уравнения асимптот l1 : у = 
х, l2 : у = - х, Оу – мнимая ось симметрии.
7. Фокальное расстояние равно 
, уравнения асимптот: l1 : у = 
х, l2 : у = - х, Оу – мнимая ось симметрии.
8. Мнимая полуось равна 6, уравнения директрис d1: х - 
, d2: х + .
9. Гипербола проходит через точку М (3 ; -6), уравнения асимптот l1 : у = 2 х, l2 : у = -2 х, Оу – мнимая ось симметрии.
10. Фокальное расстояние равно 
, уравнения асимптот: l1 : у = х, l2 : у = - х, Оу – мнимая ось симметрии.
11. Мнимая полуось равна , уравнения директрис d1: х - 
, d2: х + .
12. Фокальное расстояние равно 
, уравнения асимптот: l1 : у = 
х, l2 : у = - х, Оу – мнимая ось симметрии.
13. Мнимая полуось равна 
, уравнения директрис d1: х - 
, d2: х + .
14. Фокальное расстояние равно 
, уравнения асимптот: l1 : у =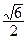 
х, l2 : у = - 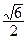х, Оу – мнимая ось симметрии.
15. Мнимая полуось равна 1, уравнения директрис d1: х - 
, d2: х + .
16. Фокусы имеют координаты F 1(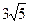
; 0), F 2(- 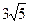; 0), уравнения асимптот: l1 : у = 2 х, l2 : у = -2 х.
17. Фокальное расстояние равно 
, уравнения асимптот: l1 : у =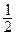 
х, l2 : у = - 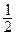х, Оу – мнимая ось симметрии.
18. Мнимая полуось равна 
, уравнения директрис d1: х - 
, d2: х + .
19. Фокусы имеют координаты F 1(
; 0), F 2(- ; 0), уравнения асимптот: l1 : у = х, l2 : у = - х.
20. Фокальное расстояние равно 12, уравнения асимптот: l1 : у = 
х, l2 : у = - х, Оу – мнимая ось симметрии.
21. Фокусы имеют координаты F 1(; 0), F 2(- ; 0), уравнения асимптот: l1 : у = 
х, l2 : у = - х.
22. Фокальное расстояние равно 
, уравнения асимптот: l1 : у = х, l2 : у = - х, Оу – мнимая ось симметрии.
Найдите каноническое уравнение эллипса и изобразите этот эллипс, его фокусы и директрисы, если известно, что:
23. Малая полуось равна 3, уравнения директрис d 1: х - 
,
d 2: х + 
.
24. Малая полуось равна 4, эксцентриситет равен 
.
25. Малая полуось равна 4, уравнения директрис d 1: х - 
, d 2: х + .
26. Малая полуось равна 3, эксцентриситет равен 
.
27. Эллипс проходит через точку М (
; -1), эксцентриситет равен .
28. Малая полуось равна 3, уравнения директрис d 1: х - 
,
d 2: х + .
29. Эллипс проходит через точку М (-4; 1), эксцентриситет равен .
30. Малая полуось равна , уравнения директрис d 1: х - 
, d 2: х + .
Вариант 31
Найдите каноническое уравнение эллипса и изобразите этот эллипс, его фокусы и директрисы, если известно, что: точка М (1; 
) принадлежит эллипсу, а директрисы имеют уравнения: d 1: х -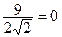 
, d 2: х + 
.
Решение. Каноническое уравнение эллипса имеет вид: 
. Чтобы найти а и b, составим систему трех уравнений с тремя неизвестными а, b и с. Первое уравнение получается из условия, что точка М (1; 
) принадлежит эллипсу. Это означает, что ее координаты удовлетворяют уравнению эллипса, т.е. 
или 
.
Второе уравнение системы получается из условия, что директрисы имеют уравнения 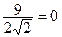х - и х + 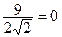. Учитывая, что уравнения директрис имеют вид 
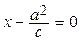и 
, получаем: 
.
В качестве третьего уравнения системы берется уравнение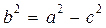 
.
Таким образом, имеем систему: 
Возведем второе уравнение в квадрат, затем вместо с 2 подставим в него 
из третьего уравнения. Далее выразим из первого уравнения b 2и подставим это в полученное уравнение. После преобразований получим уравнение 8 а 4 - 89 а 2 + 153 = 0, откуда а 2 = 9 или а 2 = 
. Из первого уравнения системы находим b 2= 1 или b 2 = 
.
Тогда каноническое уравнение эллипса будет иметь вид: 
или 
В первом случае а = 3, b = 1, с = , F 1(; 0), F 2(- ; 0).
Во втором случае а = 
, b = 
, с = 
, F 1(; 0), F 2(- ; 0).
Построим изображение эллипса, заданного первым уравнением (рис. 22).
 |
Ответ: 
, 
.
Дата публикования: 2015-11-01; Прочитано: 450 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
