Индивидуальное задание № 17

Дан куб АВСDА ₁ В ₁ С ₁ D ₁ с ребром а. Докажите, что прямые MN и PK скрещиваются и найдите угол и расстояние между ними, если:

1. М – середина А ₁ D ₁; N Î CC ₁; CN: CC ₁ = 3: 1; P – середина DD ₁; К Î ВС, ВК: КС = 2: 1.

2. М – середина ВВ ₁; N – середина А ₁ D ₁; Р Î АD, АР: АD = 2:5; К совпадает с В.

3. М совпадает с А ₁; N Î CC₁, C N: N C₁ = 1: 3; Р Î АВ, АР: РВ = 1: 2; К совпадает с С.

4. М Î DD ₁, D М : МD ₁ = 3: 2; N – середина ВС; Р Î АА ₁, АР: РА ₁ = 1: 2; К – середина D ₁ С ₁.

5. М Î ВС ₁, ВМ : МС ₁ = 1: 2; N совпадает с D ₁; Р – середина DD ₁; К Î АВ, АК: КВ = 3: 1.

6. М Î АВ, АМ : МВ = 2: 1; N Î С ₁ D ₁, C₁ N: ND ₁ = 3: 1; Р совпадает с D; К Î ВС, ВК: КС = 2: 1.

7. М Î А ₁ D, А ₁ М : МD = 2: 3; N совпадает с В ₁; Р – середина D ₁ С ₁; К – середина ВС.

8. М Î АС, АМ : МС = 1: 2; N - середина D ₁ С ₁; Р совпадает с А ₁; К Î ВВ ₁, ВК: КВ ₁ = 3: 1.

9. М Î А ₁ В, А ₁ М : МВ = 1: 2; N совпадает с С ₁; Р совпадает с В; К Î DD ₁, DК: КD ₁ = 1: 4.

10. М Î СD, СМ : МD = 1: 3; N совпадает с А ₁; Р совпадает с С ₁; К Î ВВ ₁, ВК: КВ ₁ = 4: 1.

11. М Î В ₁ D ₁, В ₁ М : МD ₁ = 2: 1; N – середина АD; Р Î А ₁ В ₁, А ₁ Р: РВ ₁ = 3: 1; К совпадает с С.

12. М – середина ВD; N совпадает с А ₁; Р – середина А ₁ В ₁; К Î СС ₁, СК: КС ₁ = 3: 1.

13. М – середина АС; N Î А ₁ D ₁, А ₁ N: ND ₁ = 1: 2; Р совпадает с С ₁; К – середина А ₁ В ₁; К Î СС ₁, СК: КС ₁ = 3: 1.

14. М Î АС, АМ: МС = 1: 3; N - середина СС ₁; Р - середина А ₁ D ₁; К совпадает с В ₁.

15. М совпадает с D; N Î ВС, ВN: NС = 1: 2; Р – середина АD; К Î D ₁ С ₁, D ₁ К: КС ₁ = 1: 4.

16. М совпадает с А; N Î СС ₁, СN: NС ₁ = 3: 1; Р совпадает с D ₁; К – середина В ₁ С ₁.

17. М Î DС ₁, DМ : МС ₁ = 2: 1; N совпадает с В; Р - середина А ₁ D ₁; К совпадает с С.

18. М Î А ₁ В, А ₁ М : МВ = 2: 3; N – середина СС ₁; Р совпадает с D ₁; К – середина АD.

19. М Î ВD ₁, ВМ : МD ₁ = 2: 1; N - середина ВС; Р Î АА ₁, АР: РА ₁ = 1: 3; К совпадает с D.

20. М – середина СА ₁; N Î С ₁ D ₁, С ₁ N: ND ₁ = 1: 2; Р совпадает с А ₁; К – середина ВВ ₁.

21. М Î СD, СМ : МD = 2: 1; N – середина В ₁ С ₁; Р совпадает с А ₁; К – середина АВ.

22. М совпадает с В; N Î АА ₁, АN: NА ₁ = 2: 3; Р - середина В ₁ D ₁; К совпадает с С.

23. М – середина АА ₁; N – середина D ₁ С ₁; Р совпадает с В; К Î А ₁ В ₁, А ₁ К: КВ ₁ = 3: 1.

24. М Î ВD, ВМ : МD = 1: 2; N совпадает с D ₁; Р Î D ₁ С ₁, D ₁ Р: РС ₁ = 1: 3; К – середина СС ₁.

25. М – середина СD ₁; N совпадает с А ₁; Р – середина А ₁ В ₁; К Î ВС, ВК: КС = 1: 2.

26. М Î АС, АМ : МС = 3: 1; N – середина А ₁ D ₁; Р совпадает с D ₁; К Î СС ₁, СК: КС ₁ = 1: 2.

27. М совпадает с С; N – середина А ₁ D; Р совпадает с В ₁; К Î АВ, АК: КВ = 2: 3.

28. М – середина В ₁ С; N совпадает с D; Р совпадает с В; К Î АА ₁, АК: КА ₁ = 3: 1.

29. М Î АС ₁, АМ : МС ₁ = 1: 2; N – середина ВС; Р совпадает с D ₁; К Î ВВ ₁, ВК: КВ ₁ = 4: 1.

30. М Î ВD ₁, ВМ : МD ₁ = 1: 3; N совпадает с С ₁; Р Î АА ₁, АР: РА ₁ = 4: 1; К – середина АВ.

Вариант 31

М Î DВ ₁, DМ : МВ ₁ = 3: 4; N Î DС, DN: NС = 4: 1; Р совпадает с А; К Î А ₁ D ₁, А ₁ К : КD ₁ = 2: 5.

Решение. Отметим на чертеже точки M, N, P и K (рис.21). Выберем прямоугольную систему координат Аi j k, где i – единичный вектор, сонаправленный с вектором АВ, j - единичный вектор, сонаправленный с вектором АD, k - единичный вектор, сонаправленный с вектором АА 1. Найдем координаты точек M, N, P и K. Так как Р совпадает с А, то Р (0; 0; 0). Координаты точки К легко найти, пользуясь определением: АК = АА 1 + А 1 К = ak + j = = (0; ; а) Þ К (0; ; а). Аналогично нахо­дим

D1 С1     К А1 В1 М   D С N k j A P i B Рис. 21

координаты точки N: AN = AD + DN = aj + i = (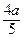; a; 0) Þ N (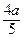; a; 0).

Найдем координаты точки М, пользуясь формулами деления отрезка в данном отношении в координатах. Так как DМ = МВ ₁, то l_М = . Учитывая, что D (0; а; 0), В ₁(а; 0; а), получи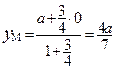м: ; ; Þ Þ М (; ; ).

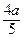Итак, прямая РК задается точкой Р (0; 0; 0) и направляющим вектором РК = (0; ; а), а прямая MN – точкой N (; a; 0) и направляющим вектором MN = ().

а) Докажем, что прямые РК и MN скрещиваются. PN = (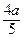; a; 0). Тогда PK × MN × PN = = ¹ 0, следовательно, MN скрещивается с РК.

б) cos(MN, PK) = . cos (MN, PK) = 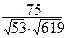Þ (MN, PK) = arccos .

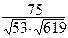в) Проведем через прямую MN плоскость g, параллельную прямой РК. Тогда r (PK, MN) = r (P, g). Найдем уравнение плоскости g:

g:	После преобразований (проделайте их самостоятельно) получаем: g: 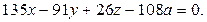Тогда r (PK, MN) = .

Ответ: (MN, PK) = arccos 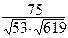; r (PK, MN) = .