Индивидуальное задание № 19

Найдите каноническое уравнение параболы, вершина которой находится в начале координат, и изобразите эту параболу, ее фокус и директрису, если известно, что:

1. Фокус имеет координаты F (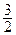; 0).

2. Уравнение директрисы d: x 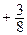= 0.

3. Парабола проходит через точку М (2; -2 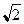), Ох – ось параболы.

4. Фокус имеет координаты F (1; 0).

5. Уравнение директрисы d: x 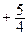= 0.

6. Парабола проходит через точку М (3; -2 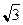), Ох – ось параболы.

7. Фокус имеет координаты F (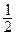; 0).

8. Уравнение директрисы d: x 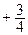= 0.

9. Парабола проходит через точку М (2; - 4), Ох – ось параболы.

10. Фокус имеет координаты F (2; 0).

11. Уравнение директрисы d: x 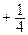= 0.

12. Парабола проходит через точку М (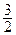; -2 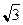), Ох – ось параболы.

13. Фокус имеет координаты F (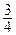; 0).

14. Уравнение директрисы d: x 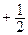= 0.

15. Парабола проходит через точку М (1; -2), Ох – ось параболы.

16. Фокус имеет координаты F (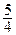; 0).

17. Уравнение директрисы d: x + 1 = 0.

18. Парабола проходит через точку М (2; -2 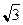), Ох – ось параболы.

19. Фокус имеет координаты F (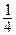; 0).

20. Уравнение директрисы d: x + 2 = 0.

21. Парабола проходит через точку М (5; - 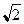), Ох – ось параболы.

22. Фокус имеет координаты F (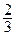; 0).

23. Уравнение директрисы d: x 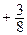= 0.

24. Парабола проходит через точку М (6; -3), Ох – ось параболы.

25. Фокус имеет координаты F (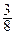; 0).

26. Уравнение директрисы d: x 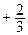= 0.

27. Парабола проходит через точку М (3; -2), Ох – ось параболы.

28. Фокус имеет координаты F (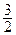; 0).

29. Уравнение директрисы d: x 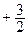= 0.

30. Парабола проходит через точку М (3; - 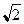), Ох – ось параболы.

Вариант 31

Уравнение директрисы d: x .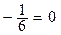

Решение. Так как уравнение директрисы x 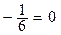, то фокус F имеет координаты (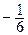; 0). Поэтому парабола симметрична относительно оси Ох и ветви ее направлены в сторону, противоположную положительному направлению оси Ох. Тогда каноническое уравнение параболы имеет вид: у ² = - 2 рх. В этом случае F 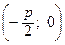и d: х - 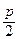= 0. Следовательно, - 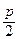= 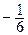, т.е. р = 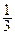. Получаем каноническое уравнение параболы: у ² = - 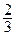х.

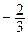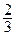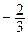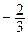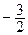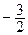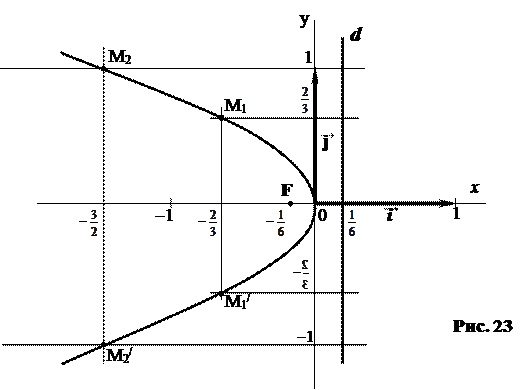
При построении изображения параболы будем пользоваться четырьмя ее вспомогательными точками: М ₁(; ); М ₁^/(; ); М ₂(; 1); М ₂^/ (; -1). Изображение параболы у ² = - 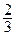х, ее фокуса и директрисы дано на рис. 23.

Ответ: у ² = - 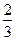х.