 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Индивидуальное задание № 12
|
|
Найдите полярные координаты точки М, заданной прямоугольными декартовыми координатами (не выполняя построения точки М):
1. М (-1; 1).
2. М (1; -1).
3. М (-1; -1).
4. М (1; - 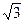 ).
5. М (-1; ).
5. М (-1; 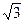 ).
6. М (-1; - ).
6. М (-1; - 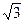 ).
7. М ( ).
7. М (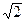 ; - ; - 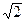 ).
8. М (- ).
8. М (- 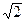 ; ; 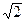 ).
9. М (- ).
9. М (- 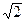 ; - ; - 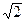 ).
10. М (-2; 2 ).
10. М (-2; 2 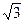 ). ).
| 11. М (2; -2 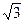 ).
12. М (-2; -2 ).
12. М (-2; -2 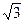 ).
13. М ( ).
13. М (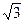 ; -1).
14. М (- ; -1).
14. М (- 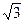 ; 1).
15. М (- ; 1).
15. М (- 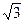 ; -1).
16. М (3; -3 ; -1).
16. М (3; -3 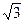 ).
17. М (-3; 3 ).
17. М (-3; 3 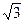 ).
18. М (-3; -3 ).
18. М (-3; -3 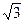 ).
19. М (2 ).
19. М (2 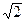 ; -2 ; -2 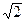 ).
20. М (-2 ).
20. М (-2 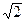 ; 2 ; 2 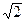 ). ).
| 21. М (-2 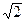 ; -2 ; -2 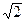 ).
22. М (2; -2).
23. М (-2; 2).
24. М (-2; -2).
25. М (-3; 3).
26. М (3; -3).
27. М (-3; -3).
28. М (-2 ).
22. М (2; -2).
23. М (-2; 2).
24. М (-2; -2).
25. М (-3; 3).
26. М (3; -3).
27. М (-3; -3).
28. М (-2 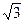 ; 2).
29. М (2 ; 2).
29. М (2 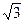 ; -2).
30. М (-2 ; -2).
30. М (-2 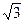 ; -2). ; -2).
|
Вариант 31
М (5 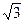 ; 5)
; 5)
Решение. Найдем полярный радиус точки М:
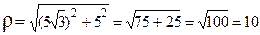 . Найдем синус и косинус полярного угла j:
. Найдем синус и косинус полярного угла j:
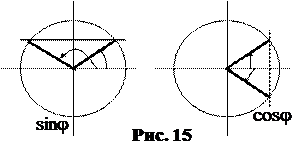  .
Так как sin j > 0, то угол j находится в первой или второй четверти тригонометрического круга, т.е. должен быть равен .
Так как sin j > 0, то угол j находится в первой или второй четверти тригонометрического круга, т.е. должен быть равен 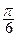 или или 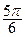 (рис.15). (рис.15).
| + + – + – – – + |
Так как cos j > 0, то угол j находится в первой или четвертой координатной четверти тригонометрического круга, т.е. должен быть равен 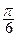 или -
или - 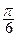 (напомним, что полярный угол j - это направленный угол и -p < j £ p) (рис.15).
(напомним, что полярный угол j - это направленный угол и -p < j £ p) (рис.15).
Выбирая общее решение делаем вывод, что j = 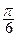 .
.
Ответ: М (10; 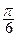 ).
).
Прямая линия на плоскости. Прямые и плоскости
В пространстве
Дата публикования: 2015-11-01; Прочитано: 324 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
