Индивидуальное задание № 10

АВСD – квадрат со стороной а, О – точка пересечения его диагоналей. Напишите формулы преобразования координат при переходе от старой прямоугольной системы координат к новой, если даны оси (т.е. направленные прямые) старой и новой систем:

1. ВА, АD – оси старой системы, СА, DВ – новой.

2. АС, ВD – оси старой системы, СВ, ВА – новой.

3. СD, АD – оси старой системы, АВ, ВС – новой.

4. ВС, АВ – оси старой системы, DВ, СА – новой.

5. СВ, DС – оси старой системы, СА, DВ – новой.

6. DА, ВА – оси старой системы, DС, СВ – новой.

7. СА, ВD – оси старой системы, СD, ВС – новой.

8. АD, СD – оси старой системы, СD, СВ – новой.

9. DА, АВ – оси старой системы, СD, АD – новой.

10. СВ, DС – оси старой системы, СD, DА – новой.

11. DВ, СА – оси старой системы, ВА, DА – новой.

12. ВА, АD – оси старой системы, АВ, ВС – новой.

13. DА, DС – оси старой системы, АВ, ВС – новой.

14. DА, ВА – оси старой системы, АС, ВD – новой.

15. DВ, СА – оси старой системы, АD, АВ – новой.

16. АС, ВD – оси старой системы, СВ, АВ – новой.

17. ВА, DА – оси старой системы, СА, DВ – новой.

18. ВС, DС – оси старой системы, ВА, АD – новой.

19. АD, DС – оси старой системы, СА, ВD – новой.

20. ВА, АD – оси старой системы, СА, DВ – новой.

21. ВА, АD – оси старой системы, АD, СD – новой.

22. АС, ВD – оси старой системы, DА, СD – новой.

23. ВА, DА – оси старой системы, DС, АD – новой.

24. ВС, СD – оси старой системы, АВ, АD – новой.

25. DВ, СА – оси старой системы, АВ, ВС – новой.

26. ВА, АD – оси старой системы, СD, СВ – новой.

27. АС, ВD – оси старой системы, ВС, DС – новой.

28. СD, АD – оси старой системы, DА, АВ – новой.

29. ВС, АВ – оси старой системы, СD, DА – новой.

30. DА, DС – оси старой системы, АВ, СВ – новой.

Вариант 31

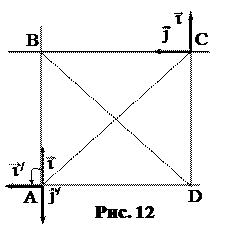DС, СВ – оси старой системы, DА, ВА – новой.

Решение. Начало старой прямоугольной системы координат – это точка пересечения прямых ДС и СВ, т.е. точка С. Так как DС и СВ - направленные прямые, то первый координатный вектор i старой системы исходит из точки С и сонаправлен с вектором DС (рис.12), второй координатный вектор j тоже исходит из точки С и сонаправлен с вектором СВ. Следовательно, система С i j – правая.

Аналогично находим новое начало: DА Ç ВА = А, i ^/ сонаправлен с DА, j ^/ - с ВА. Система А i ^/ j ^/ - правая (рис.12).

Запишем формулы преобразования прямоугольной системы координат:

где х₀, у₀ - координаты точки А в системе С i j, a - направленный угол между векторами i и i ^/.

Найдем e, х₀, у₀ и a. Так как старая и новая системы одинаково ориентированы (обе правые), то e = 1.

Найдем координаты радиус-вектора СА точки А в старой системе: СА = СD + СВ = - аi + а j = (- а; а). Следовательно, А (-а; а), т.е. х₀ = -а, у₀ = а.

Чтобы найти направленный угол a, приведем векторы i и i ^/ к общему началу С или А. Тогда a = + .

Формулы преобразования координат примут вид:

или

Ответ: