При параллельном переносе и повороте осей

Пусть у какого-нибудь сечения площадью F (рис. 16) ось X будет центральной, а ось Х₁ - параллельная ей на расстоянии a. Выделим в сече­нии элементарную площадку dF на расстоянии у от оси х, тогда рас­стояние площадки dF от оси X₁ бу­дет y₁ = у + а.

Напишем выражение момента инерции площади сечения относительно оси Х₁:

.

В полученном выражении первый интеграл представляет собой осевой момент инерции относительно оси X, проходящей через центр тяжести, т.е. , второй интеграл выражает собой статический момент всей площади сечения отно­сительно оси, проходящей через центр тяжести сечения, и, следовательно, рав­ный нулю, т.е. .

Последний интеграл выражает собой площадь всего сечения F. Таким образом, момент инерции сечения относительно оси X₁:

. (14.1)

Полученная формула читается так: момент инерции площади сечения отно­сительно любой оси равен моменту инерции относительно оси, ей параллельной и проходящей через центр тяжести сечения, плюс произведение площади сечения на квадрат расстояния между осями. При помощи этой формулы можно вычислить мо­менты инерции любого сложного сечения.

Аналогично записываются формулы перехода для осевого и центробеж­ного моментов инерции:

, (14.2)

. (14.3)

В формулах (14.1) и (14.3) величина а - расстояние от центральной оси инерции X до оси Х₁, а величина b - расстояние от центральной оси инерции у до оси у₁.

Для определения момента инерции сложного сечения его разбивают на элемен­тарные сечения (прямоугольники, треугольники и т.д.), затем вычисляют моменты инерции элементарных сечений относительно центральной оси сложного сечения и суммируют их.

Приведем без доказательства формулы перехода для моментов инерции при повороте осей на некоторый угол α. Предположим, что какое-нибудь сечение имеет моменты инерции , , относительно осей координат X,У (рис.17). Требуется определить моменты инерции того же сечения относитель­но осей Х₁ У₁, повернутых на некоторый угол α(рис.17).

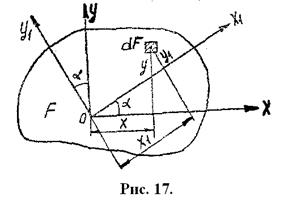Моменты инерции сечения относительно нового положения осей определяются по формулам:

,(14.4)

,(14.5)

(14.6)