Моменты инерции, моменты сопротивления и радиусы инерции

Плоских сечений

Осевым моментом инерции плоского сечения относительно данной оси называ­ется взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадраты их расстояний до этой оси:

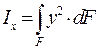(см⁴), (13.1)

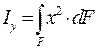(см⁴). (13.2)

Осевые моменты инерции всегда положительны и не могут быть равны нулю.

Центробежным моментом инерции плоского сечения называется взятая по всей площади сечения сумма произведений площадей элементарных площадок на их рас­стояния до двух взаимно перпендикулярных осей:

(см⁴). (13.3)

Центробежный момент инерции может быть положительным, отрицательным и равным нулю.

Осевые и центробежные моменты инерции плоского сечения относительно осей, параллельных центральным осям, определяют по формулам:

, (13.4)

, (13.5)

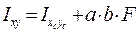, (13.6)

где и - осевые моменты инерции относительно центральных осей;

- центробежный момент инерции относительно центральных осей;

a, b - расстояния между выбранными осями и параллельными им цент­ральными осями.

При повороте осей на угол α моменты инерции определяют по формулам:

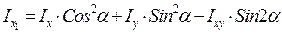, (13.7)

, (13.8)

. (13.9)

Когда значение угла поворота осей достигнет величины, определяемой формулой:

, (13.10)

тогда осевые моменты инерции достигают своего максимума и минимума, а центро­бежный момент инерции становится равным нулю. Оси, занимающие такое положение, называются главными осями инерции, а соответствующие экстремальные осевые мо­менты инерции - главными моментами инерции. Главные оси инерции, проходящие через центр тяжести плоского сечения, называются главными центральными осями инерции.

Величину главных моментов инерции определяют по формуле:

. (13.11)

Моментом сопротивления сечения называется отношение осевого момента инерции к расстоянию от нейтральной оси до наиболее удаленной точки сечения:

(см³), (13.12)

(см³). (13.13)

Радиусом инерции сечения относительно оси называется величина, опреде­ляемая по формуле:

(см), (13.14)

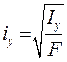(см). (13.15)