Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Вид частных решений, характеристическое уравнение

ЛОДУ с постоянными коэффициентами

у⁽ⁿ⁾ + P₁y^(n-1) +…+ P_n-1 y’ + P_n y = 0, где все P_i (i= 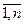)= const

будем искать частное решение y=e^kx, к – неизвестная постоянная

y’=ke^kx

y’’=k²e^kx

……

y⁽ⁿ⁾=k⁽ⁿ⁾ e^kx

k⁽ⁿ⁾ e^kx + P₁k^(n-1) e^kx + … + P_ne^kx = e^kx(k⁽ⁿ⁾ + P₁k^(n-1) + … + P_n) = 0

e^kx 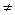0 => k⁽ⁿ⁾ + P₁k^(n-1) + … + P_n = 0, (1)

ð y=e^kx - решение ДУ

(1) – характеристическое уравнение для ЛОДу с постоянными коэффициентами, выражения слева характеристический многочлен.

Решением характеристич уравнения (1) дает систему частных решений ЛОДу, структура ФСР зависит от вида корней характер уравнения.

(1) – алгебраическое уравнение n-ой степени, может иметь не более, чем n корней, обознач-м эти корни характеристического уравнения через k₁,k₂ …k_n

Возможны случай

1)все корни хар-го уранения вещественны и различны

2)все корни различны, но среди них есть комплексные

3)среди действительных корней имеются кратные

4)среди комплексных корней есть кратные

Общий алгоритм решения ЛОДу с постоянным коэффициентом

1) составим характер уравнение: y=e^kx, k⁽ⁿ⁾ + P₁k^(n-1) + … + P_n = 0

2) найти корни характер уравнения k₁,k₂ …k_n

3) по характеру корней находим частное линейно-независимое решение по таблице 1

4) подставляем частное решение 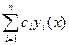на основе Теоремы о структуре общего решения ЛОДУ и получаем общее решение y =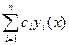

№	Вид корня	Соответственное решение
	Действ корень кратности 1	ekx
	Пара корней a bi;кратнос 1	eаxcosbx, eаxsinbx
	Действит корень кратност α	ekx, хekx, х2ekx, х3ekx,…, хα-1ekx
	Пара сопряж корней α a bi	eаxcosbx, eаxsinbx хeаxcosbx, хeаxsinbx х2eаxcosbx, х2eаxsinbx хα-1eаxcosbx, хα-1eаxsinbx