Свойства определенного интеграла от чет. и нечт. функции на симметричном промежутке

Если функция f(x) чётная на отрезке [-a;a], то

Если функция f(x) нечётная на отрезке [-a;a], то

Понятие общего решения дифференциального уравнения первого порядка, частное решение, начальные условия, задача Коши.

Опр. Общим решением (общим интегралом) уравнения (1) называется такое соотношение (2), что:

1. Любое решение (2) относительно y (для набора постоянных C ₁, C ₂, …, C_n из некоторой области n -мерного пространства) - частное решение уравнения (1);
2. Любое частное решение уравнения (1) может быть получено из (2) при некотором наборе постоянных C ₁, C ₂, …, C_n.
Мы будем в основном рассматривать дифференциальные уравнения в форме, разрешённой относительно старшей производной: 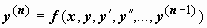(3) и получать общее решение в форме (4) решённой относительно неизвестной функции.

Опр. Частным решением уравнения (1) на интервале (a, b) (конечном или бесконечном) называется любая n раз дифференцируемая функция , удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество. Так, функция y (x) = e^x + x обращает уравнение: y ⁽⁴⁾ – y + x = 0 в тождество на всей числовой оси (y ⁽⁴⁾(x) = e^x; e^x –(e^x + x) + x = 0), т.е. является частным решением этого уравнения. Любое уравнение порядка имеет множество частных решений (частным решением приведённого уравнения является и функция y (x) = sin(x) + x). Процедуру решения дифференциального уравнения часто называют интегрированием уравнения, при этом интегрировать приходится в общем случае ровно n раз, и при каждом интегрировании в решение входит очередная произвольная постоянная.

Задача Коши (задача с начальным условием). Пусть функция f (x, y) определена в области D, точка . Требуется найти решение уравнения ; (8) удовлетворяющее начальному условию y (x ₀) = y ₀; (9) (начальное условие (9) часто записывают в форме ).
Теорема Коши (существования и решения задачи Коши). Если в области D функция f (x, y) непрерывна и имеет непрерывную частную производную , то для любой точки в окрестности точки x ₀ существует единственное решение задачи ((8),(9)).

23. Теорема о существовании и единственности решения ДУ в полных дифференциалах.

24. Определитель Вронского.

Определитель Вронского — определитель следующей матрицы:

Применяется для решения дифференциальных уравнений.

Имеют место следующие теоремы: Пусть y₁(x),…,y_n(x) — (n-1) раз дифференцируемые функции, тогда:

· Если y₁(x),…,y_n(x) линейно зависимы на X, то det(W) = 0.

· Если det(W) = 0 хотя бы для одного , то y₁(x),…,y_n(x) линейно зависимы на X.

Или:

· Определитель Вронского либо тождественно равен нулю, и это означает, что y₁(x),…,y_n(x) линейно зависимы, либо не обращается в нуль ни в одной точке X, что означает линейную независимость функций y₁(x),…,y_n(x).