Равномерная сходимость функционального ряда

Функциональный ряд u_n(x) называется равномерно сходящимся в некоторой области x, если для каждого сколь угодно малого числа >0 найдётся такое целое положительное число N(), что при n>N выполняется неравенство = < для всех x из области X.

При этом сумма S(x) равномерно сходящегося функционального ряда есть непрерывная функция.

Достаточным признаком равномерности сходимости является - Признак Вейерштрасса.

31. Теорема и признак Вейерштрасса:

Признак Вейерштрасса.

Если члены функционального ряда U1(x)+U2(x)+…+Un(x)+… по абсолютной величине не превышают в некоторой области соответствующих членов сходящегося знакоположительного ряда a1+ a2+…+an+…, т.е.

|U1(x)| a1, |U2(x)| a2, |U3(x)| a3, … |Un(x)| an, …

То функциональный ряд в области сходиться абсолютно и равномерно (правильно).

Знакоположительный числовой ряд называется мажорирующим рядом или мажорантой для данного функционального ряда.

Т. Вейерштрасса. Если существует такая числовая последовательность {an}, что =0, аn (1),

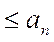(2) для всех n=1,2… и всех х , то последовательность { } равномерно на E сходится к функции .

Доказательство. В силу условия (1) для любого существует такой номер , что an< для всех 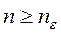. Но тогда в силу условия (2) для всех и всех х , а это и означает равномерную сходимость последовательности { } к функции на множестве Е.