Понятие несобственного интеграла II рода

Пусть функция 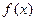непрерывна на промежутке 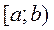и имеет бесконечный разрыв при x=b. Если существует конечный предел 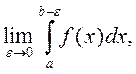то его называют несобственным интегралом второго рода и обозначают 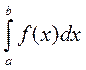. Таким образом, по определению, 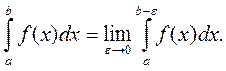Если предел в правой части существует, то несобственный интеграл 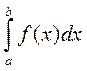сходится. Если же указанный предел не существует или он бесконечен, то говорят, что интеграл 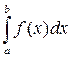расходится. Аналогично, если функция 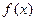терпит бесконечный разрыв в точке x=a, то полагают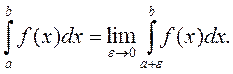

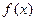Если функция терпит разрыв во внутренней точке c отрезка 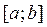, то несобственный интеграл второго рода определяется формулой 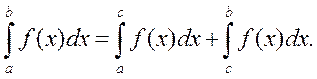В этом случае интеграл слева называют сходящимся, если оба несобственных интеграла, стоящих справа, сходятся. В случае, когда 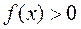, несобственный интеграл второго рода 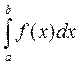(разрыв в точке x=b) можно истолковать геометрически как площадь бесконечно высокой криволинейной трапеции.