Нахождение коэффициентов для тригонометрического р. Фурье (теорему док)

Теорема: Если ф-ия 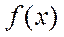определена на 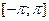и разлагается в тригонометрический ряд (*), к-е можно почленно интегрировать, то это разложение единственное.

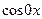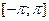
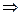
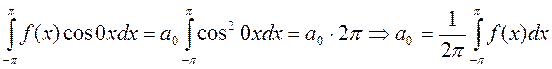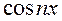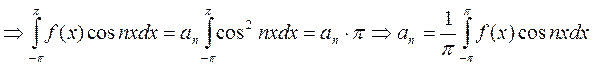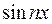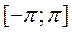
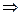
Доказательство: Умножим обе части (*) на , проинтег-ем на . Аналогично умножим (*) на и проинтег-ем. . Умножим (*) на и проинтег-ем на 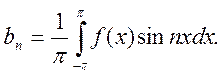Коэфф-ты рав-ва (*) опр-ся единственным образом 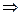такое разложение единственное 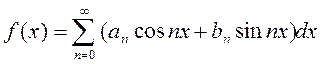, , 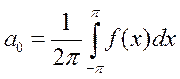, 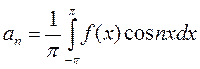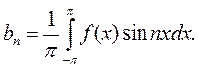Теорема доказана.