 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Степенные ряды. Теорема Абеля. Радиус сходимости
|
|
Функциональные ряды вида 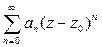 , где an, z, z0 – комплексные числа, называются степенными рядами. Числа an, n=0,1,2…называются коэффициентами степенного ряда.
, где an, z, z0 – комплексные числа, называются степенными рядами. Числа an, n=0,1,2…называются коэффициентами степенного ряда.
Т. Абеля. Если степенной ряд 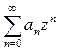 (1) сходится при z=z0, то он сходится и при том абсолютно при любом z, у которого
(1) сходится при z=z0, то он сходится и при том абсолютно при любом z, у которого 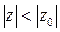 .
.
Доказательство. Пусть ряд 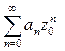 (2) сходится, тогда его n-ый член
(2) сходится, тогда его n-ый член 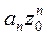 стремиться к нулю при
стремиться к нулю при 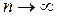 и поэтому последовательность
и поэтому последовательность
{ 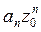 } ограничена, т.е. существует такая постоянная M>0, что
} ограничена, т.е. существует такая постоянная M>0, что 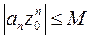 , а n=0,1,2… В силу этого для n-го члена ряда (1) получается следующая оценка:
, а n=0,1,2… В силу этого для n-го члена ряда (1) получается следующая оценка: 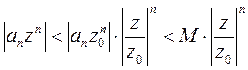 . Если
. Если 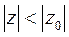 , то ряд
, то ряд 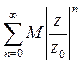 , являясь геометрической прогрессией со знаменателем
, являясь геометрической прогрессией со знаменателем  <1, сходится. Поэтому по признаку сравнения сходится и ряд
<1, сходится. Поэтому по признаку сравнения сходится и ряд 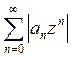 , а это означает абсолютную сходимость ряда (1) при
, а это означает абсолютную сходимость ряда (1) при 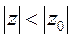 . Теорема доказана.
. Теорема доказана.
У всякого степенного ряда 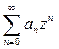 существует радиус сходимости R. В круге сходимости, т.е. при любом z, у которого
существует радиус сходимости R. В круге сходимости, т.е. при любом z, у которого 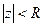 , ряд
, ряд 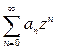 сходится абсолютно. На любом круге
сходится абсолютно. На любом круге 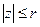 , где r фиксировано и r<R, ряд сходится равномерно. Пусть R- радиус сходимости степенного ряда
, где r фиксировано и r<R, ряд сходится равномерно. Пусть R- радиус сходимости степенного ряда 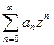 , тогда R =
, тогда R = 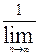
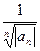 .
.
Дата публикования: 2015-10-09; Прочитано: 600 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
