 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема о суперпозиции решений (принцип сложения решений)
|
|
Если функция yi(x) является решением ЛНДУ
(3) y(n) + P1y(n-1) + … + Pny = fi(x) то функция 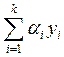 = α1y1 + α2y2 + … + αnyn, то это функция является решением y(n) + P1y(n-1) + … + Pny = α1 f1(x) + α2 f2(x) + … + αn fn(x) (4)
= α1y1 + α2y2 + … + αnyn, то это функция является решением y(n) + P1y(n-1) + … + Pny = α1 f1(x) + α2 f2(x) + … + αn fn(x) (4)
Док-во: для n=2
y = α1y1 + α2y2
y’ = α1y1’ + α2y2’
y’’ = α1y1’’ + α2y2’’
Подставим y, y’, y”, в (4), учитываем что y1 y2 решение соответственного уравнения (3)
α1y1” + α2y2” + P1(x)[ α1y1’+ α2y2’] + P2(x)[ α1y1+ α2y2] =
= [α1y1” + P1(x)α1y’1 + P2(x)α1y1] + [α2y2” + P1(x)α2y’2 + P2(x)α2y2] = α1f1(x) + α2f2(x)
 |
16. Метод вариации произвольных постоянных – метод Лагранжа
Метод позволяет найти решение ДУ независимо от вида правой части, когда известно общее решение соотв-го однородного ДУ.
ДУ 2-го порядка. Пусть y”+P1(x)y’+P2(x)y=f(x) (1) пусть y1(x) и y2(x) - ФСР ЛОДУ
y”+P1(x)y’+P2(x)y=0 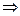
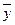 (x)= C1y1(x)+C2y2(x) (2). Частное решение y*(x) в виде (14) считая при этом C1 и C2 не постоянными, а неизвестными функциями от x.
(x)= C1y1(x)+C2y2(x) (2). Частное решение y*(x) в виде (14) считая при этом C1 и C2 не постоянными, а неизвестными функциями от x.
y*= C  (x)y
(x)y  (x)+C
(x)+C  (x)y
(x)y  (x), y*= C’
(x), y*= C’  (x)y
(x)y  (x)+C(x)
(x)+C(x)  y’
y’  (x)+C’
(x)+C’  (x)y
(x)y  (x)+ C(x)
(x)+ C(x)  y’
y’  (x)
(x)
Пусть C  (x) и C
(x) и C  (x)
(x) 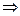 C’
C’  (x)y
(x)y  (x)+ C’
(x)+ C’  (x)y
(x)y  (x)=0 /справедливое равенство (3), тогда y* ’= C
(x)=0 /справедливое равенство (3), тогда y* ’= C  (x)y’
(x)y’  (x)+ C
(x)+ C  (x)y’
(x)y’  (x); y* ”= C
(x); y* ”= C  (x)y’
(x)y’  (x)+ C
(x)+ C  (x)y”
(x)y”  (x)+ C’
(x)+ C’  (x)y’
(x)y’  (x)+ C
(x)+ C  (x)y”
(x)y”  (x).
(x).
Подставим y*, y* ’, y* ” в (1): C  (x)[ y”
(x)[ y”  (x) + P
(x) + P  (x)y
(x)y  ’(x) + P
’(x) + P  (x) y
(x) y  (x)] + C
(x)] + C  (x)[ y”
(x)[ y”  (x) + P
(x) + P  (x)y
(x)y  ’(x) + P
’(x) + P  (x) y
(x) y  (x)] + C’
(x)] + C’  (x)y’
(x)y’  (x)+ C’
(x)+ C’  (x)y’
(x)y’  (x)=f(x). Т.к. y
(x)=f(x). Т.к. y  (x), y
(x), y  (x) решения ОДУ, то выражения []=0
(x) решения ОДУ, то выражения []=0 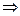 C’
C’  (x)y’
(x)y’  (x) + C’
(x) + C’  (x)y’
(x)y’  (x)=0.
(x)=0.
Объясним два условия и (3):
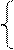 C’1(x)y1(x)+ C’2(x)y2(x)=0
C’1(x)y1(x)+ C’2(x)y2(x)=0
C’1(x)y’1(x)+ C’2(x)y’2(x)=f(x) (4)
Неопределённые функции C’1(x) и C’2(x).
Определитель этой системы: W[y1, y2]= 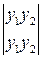
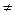 0
0 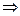 решая эту систему, мы получим C
решая эту систему, мы получим C  (x)=
(x)= 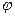 (x), C
(x), C  (x)=
(x)= 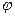 (x) проинтегрируем и получим решение
(x) проинтегрируем и получим решение 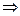 C1(x) и C2(x) найдены. Подставим в y*.
C1(x) и C2(x) найдены. Подставим в y*.
Для ЛНДУ n-го порядка ф-ии Ci(x) определяются из системы:
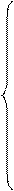 C’
C’  (x)y
(x)y  + C’
+ C’  (x)y
(x)y  +…+ C’
+…+ C’ 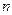 (x)y
(x)y 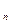 =0
=0
C’  (x)y’
(x)y’  + C’
+ C’  (x)y’
(x)y’  +…+ C’
+…+ C’ 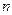 (x)y’
(x)y’ 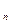 =0
=0
……………………………………………
C’  (x)y
(x)y 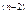
 + C’
+ C’  (x)y
(x)y 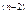
 +…+ C’
+…+ C’ 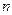 (x)y
(x)y 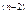
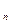 =0
=0
C’  (x)y
(x)y 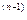
 + C’
+ C’  (x)y
(x)y 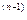
 +…+ C’
+…+ C’ 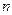 (x)y
(x)y 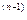
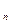 =f(x)
=f(x)
Дата публикования: 2015-10-09; Прочитано: 931 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
