 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Базис векторного пространства
|
|
Справочный материал.
Векторы 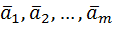 линейно независимы, если существуют такие числа
линейно независимы, если существуют такие числа 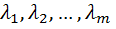 равные одновременно нулю, что
равные одновременно нулю, что
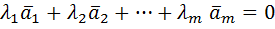 .
.
Линейное пространство 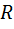 называется n-мерным, если в нём существуют n линейно независимых векторов, а любые из
называется n-мерным, если в нём существуют n линейно независимых векторов, а любые из 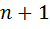 векторов являются линейно зависимыми.
векторов являются линейно зависимыми.
Совокупность n линейно независимых векторов n -мерного пространства  называется базисом.
называется базисом.
Пример. Выяснить, образуют ли базис трёхмерного линейного пространства векторы 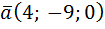 ,
, 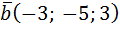 ,
, 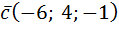 .
.
Решение. Векторы образуют базис, если они линейно независимы. Воспользуемся формулой:
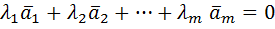 .
.
Получаем:
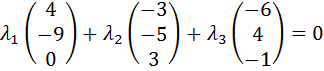 ,
,
что можно записать в виде однородной системы линейных алгебраических уравнений:
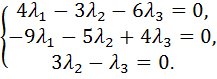
Полученная однородная система будет иметь только нулевое решение (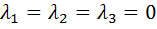 ), если определитель системы не равен нулю:
), если определитель системы не равен нулю:
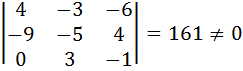 .
.
Таким образом, система имеет только нулевое решение, поэтому векторы 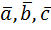 линейно независимы, а значит образуют базис.
линейно независимы, а значит образуют базис.
Ответ: да.
Задание 17. Выяснить, образуют ли базис трёхмерного линейного пространства векторы 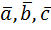 .
.
| Номер варианта | 
| 
| 
|

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |
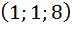
| 
| 
| |

| 
| 
| |

| 
| 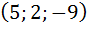
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |
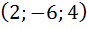
| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 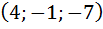
| 
| |

| 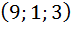
| 
| |

| 
| 
| |

| 
| 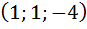
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 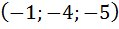
| 
| |

| 
| 
|
Дата публикования: 2015-10-09; Прочитано: 376 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
