 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Квадратичные формы
|
|
Справочный материал.
Квадратичной формой 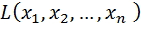 от n переменных называется сумма, каждое слагаемое которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
от n переменных называется сумма, каждое слагаемое которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
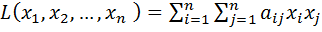 .
.
Коэффициенты квадратичной формы 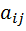 – действительные числа, причём
– действительные числа, причём 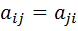 . Матрица
. Матрица 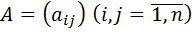 , составленная из этих коэффициентов, называется матрицей квадратичной формы.
, составленная из этих коэффициентов, называется матрицей квадратичной формы.
В матричной записи квадратичная форма имеет вид:
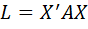 ,
,
где 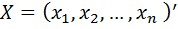 – матрица-столбец переменных,
– матрица-столбец переменных,  – матрица квадратичной формы.
– матрица квадратичной формы.
Квадратичная форма называется канонической, если все её коэффициенты 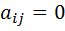 при
при 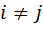 :
:
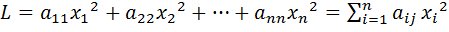 .
.
Канонический вид квадратичной формы не является однозначно определённым.
Пример. Привести квадратичную форму 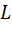 к каноническому виду:
к каноническому виду:
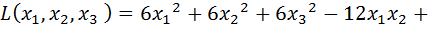
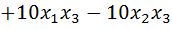 .
.
Решение.
Выполним следующие преобразования:
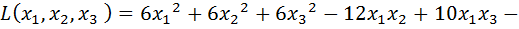
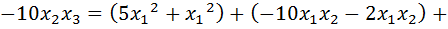
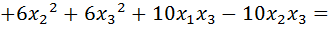
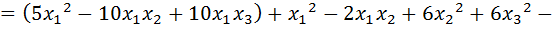
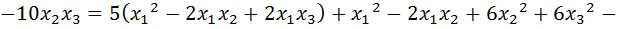
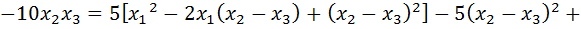
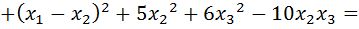
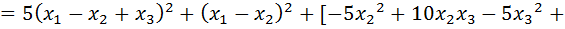
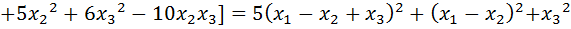 .
.
Выполним переобозначения:
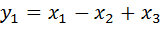 ,
, 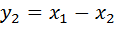 ,
, 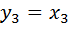 .
.
Полученное линейное преобразование 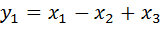 ,
, 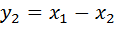 ,
, 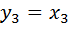 приводит квадратичную форму к следующему каноническому виду:
приводит квадратичную форму к следующему каноническому виду:
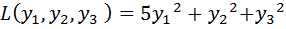 .
.
Ответ: 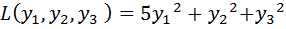 .
.
Задание 21. Привести квадратичную форму к каноническому виду.
1. 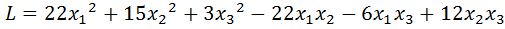 .
.
2. 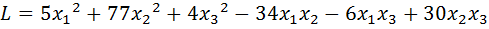 .
.
3. 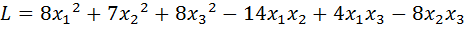 .
.
4. 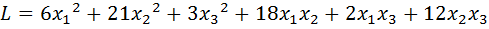 .
.
5. 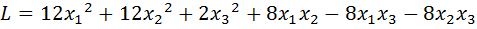 .
.
6. 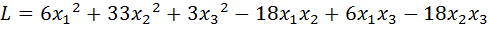 .
.
7. 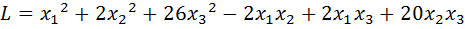 .
.
8. 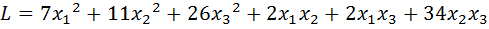 .
.
9. 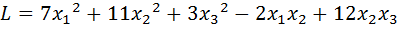 .
.
10. 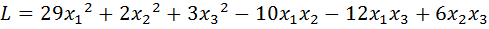 .
.
11. 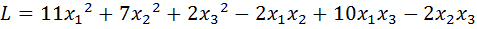 .
.
12. 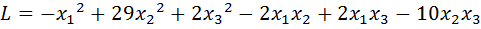 .
.
13. 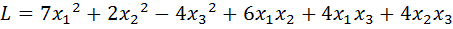 .
.
14. 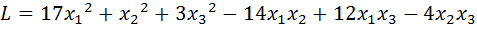 .
.
15. 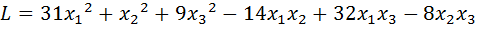 .
.
16. 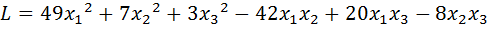 .
.
17. 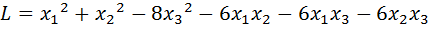 .
.
18. 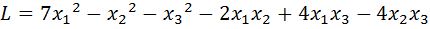 .
.
19. 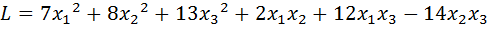 .
.
20. 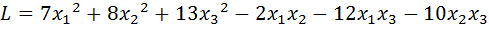 .
.
21. 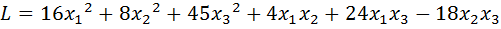 .
.
22. 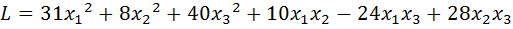 .
.
23. 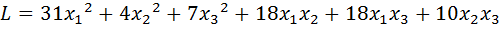 .
.
24. 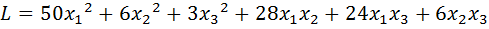 .
.
25. 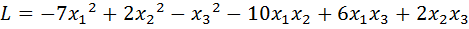 .
.
26. 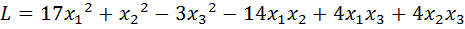 .
.
27. 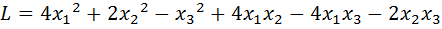 .
.
28. 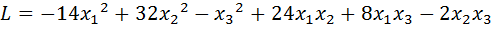 .
.
29. 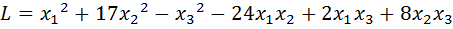 .
.
30. 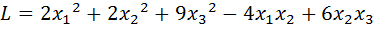 .
.
31. 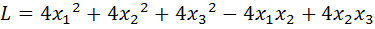 .
.
32. 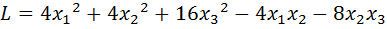 .
.
33. 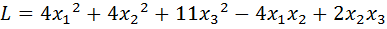 .
.
34. 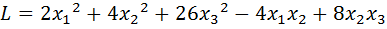 .
.
35. 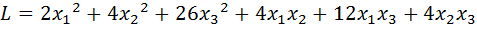 .
.
36. 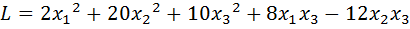 .
.
Дата публикования: 2015-10-09; Прочитано: 771 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
