 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Матричные уравнения
|
|
Справочный материал.
Простейшие матричные уравнения могут быть записаны в виде.
1. 
, где 
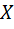– неизвестная матрица; если матрица 
– невырожденная (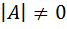
), то решение матричного уравнения записывается в виде 
.
2. 
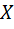, где – неизвестная матрица; если матрица – невырожденная (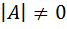), то решение матричного уравнения записывается в виде 
.
3. 
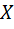, где – неизвестная матрица; если матрицы и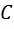 
– невырожденные (, 
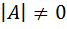), то решение матричного уравнения записывается в виде 
.
Во всех трёх случаях матрицы 
имеют такую размерность, что используемые операции умножения определены, при этом левая и правая части матричного уравнения представляют собой матрицы одинаковой размерности.
Пример. Решить матричное уравнение
.
Решение. Запишем данное уравнение в виде , где 
, 
, 
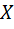, – матрица неизвестных. Решением этого уравнения является матрица
.
Найдём матрицу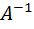 
. Используем формулу нахождения обратной матрицы: 
, где 
– определитель матрицы ; 
– алгебраические дополнения элементов матрицы .
Найдём определитель матрицы :
.
Так как матрица невырожденная, то для неё существует обратная. Найдём алгебраические дополнения элементов матрицы :
, 
, 
, 
.
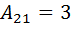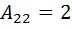Матрица, обратная для имеет вид:
.
Найдём матрицу 
.
Найдём определитель матрицы :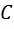
.
Так как матрица 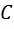невырожденная, то для неё существует обратная. Найдём алгебраические дополнения элементов матрицы :
, 
, 
, 
.
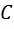Матрица, обратная для 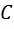имеет вид:
.
Найдём матрицу неизвестных:
.
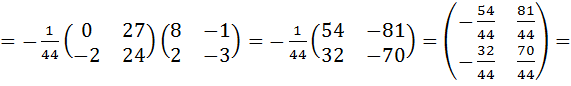
Ответ: 
.
Задание 13. Решить матричное уравнение.
1. 
.
2. 
.
3. 
.
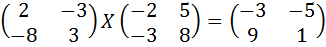4. 
.
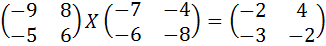5. 
.
6. 
.
7. 
.
8. 
.
9. 
.
10. 
.
11. 
12. 
.
13. 
.
14. 
.
] 15. 
.
16. 
.
17. 
.
18. 
.
19. 
.
20. 
.
21. 
.
22. 
.
23. 
.
24. 
.
25. 
.
26. 
.
27. 
.
28. 
.
29. 
.
30. 
.
31. 
.
32. 
.
33. 
.
34. 
.
35. 
.
36. 
.
Дата публикования: 2015-10-09; Прочитано: 470 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
