 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Линейная модель обмена
|
|
Справочный материал.
Линейной моделью обмена является матричное уравнение  или, что одно и то же,
или, что одно и то же,  , где
, где  – структурная матрица торговли,
– структурная матрица торговли, 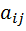 – доля национального дохода, которую страна
– доля национального дохода, которую страна  тратит на покупку товаров у страны
тратит на покупку товаров у страны 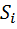 , причём
, причём  ;
;  – вектор национальных доходов стран
– вектор национальных доходов стран  ;
;  – единичная матрица,
– единичная матрица, 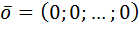 – нулевой вектор. Решить уравнение
– нулевой вектор. Решить уравнение  означает найти собственный вектор
означает найти собственный вектор  , соответствующий собственному значению
, соответствующий собственному значению  .
.
Пример. Найти соотношение национальных доходов трёх стран для сбалансированной торговли, если задана структурная матрица торговли  :
:

Решение.
Найдём собственный вектор  , отвечающий собственному значению
, отвечающий собственному значению  . Для этого решим уравнение
. Для этого решим уравнение  . Запишем матрицу
. Запишем матрицу  :
:
 .
.
Тогда уравнение  можно записать в виде следующей однородной системы линейных алгебраических уравнений:
можно записать в виде следующей однородной системы линейных алгебраических уравнений:

Выполним преобразования. Умножим первое уравнение на 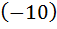 , второе и третье на 10:
, второе и третье на 10:
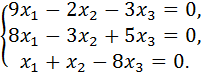
Решим систему методом Гаусса. Запишем расширенную матрицу системы:
 .
.
Приведём расширенную матрицу системы к ступенчатому виду.
1) Поменяем местами первую и третью строки:
 .
.
2) Прибавим ко второй строке первую, умноженную на  , прибавим к третьей строке первую, умноженную на
, прибавим к третьей строке первую, умноженную на 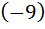 :
:
 .
.
3) Прибавим к третьей строке вторую, умноженную на  :
:
 .
.
4) Вычеркнем нулевую строку:
 .
.
5) Умножим вторую строку на  :
:
 .
.
Так как ранг матрицы системы равен 2 и ранг расширенной матрицы системы равен 2, то система совместна. И так как число неизвестных равно 3, то есть ранг меньше числа неизвестных, то система имеет бесконечное множество решений.
Запишем систему уравнений по виду последней матрицы:

Объявляем неизвестные  основными, неизвестную
основными, неизвестную 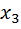 свободной. Выразим основные неизвестные через свободную. Из второго уравнения
свободной. Выразим основные неизвестные через свободную. Из второго уравнения 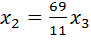 . Из первого уравнения
. Из первого уравнения  . Переобозначим неизвестное
. Переобозначим неизвестное 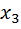 через c. Тогда решением системы является вектор
через c. Тогда решением системы является вектор  . Полученный результат означает, что сбалансированность торговли трёх стран достигается при соотношении национальных доходов стран
. Полученный результат означает, что сбалансированность торговли трёх стран достигается при соотношении национальных доходов стран  или
или  .
.
Ответ:  .
.
Задание 20. Найти соотношение национальных доходов трёх стран для сбалансированной торговли, если задана структурная матрица торговли  .
.
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 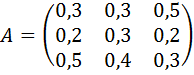
13.  14.
14. 
15. 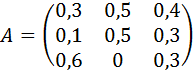 16.
16. 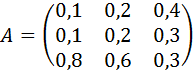
17.  18.
18. 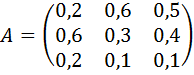
19.  20.
20. 
21.  22.
22. 
23. 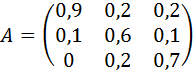 24.
24. 
25.  26.
26. 
27.  28.
28. 
29.  30.
30. 
31.  32.
32. 
33.  34.
34. 
35.  36.
36. 
Дата публикования: 2015-10-09; Прочитано: 8122 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
