Теоретичні відомості. Правило Рунге практичної оцінки похибки (правило подвійного перерахування):

Правило Рунге практичної оцінки похибки (правило подвійного перерахування):

, де , i= 1, …, N, p – порядок методу, а обчислення ведуться у вузлах сітки .

Уточнений розв'язок обчислюється по формулі: , i= 1,…, N.

Постановка задачи. Знайти приблизні значення розвязку звичайного диференціального рівняння (ЗДР) на відрізку з кроком з начальною умовою

Розрахункові формули методів розв'язку задачі Коші для ЗДР 1 порядку:

Метод розкладання по формулі Тейлора 2 порядку:

Модифікований метод Ейлера 2 порядку:

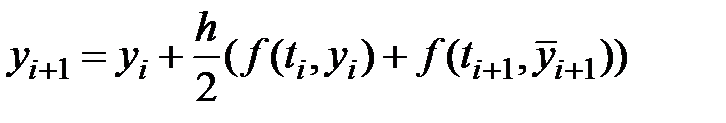
Метод Рунге-Кутти 3 порядку I: , , ,

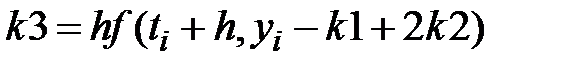Метод Рунге-Кутти 3 порядку II: , , ,

Метод Рунге-Кутти 3 порядку III: , , , 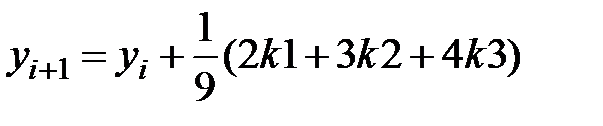Метод Рунге-Кутта четвертого порядка   ,

Экстраполяційний метод Адамса 2 порядку:

Экстраполяційний метод Адамса 3 порядку:

Экстраполяційний метод Адамса 4 порядку:

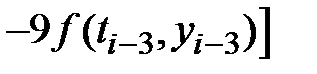
Зведення ЗДР 3 порядку до системи ЗДР 1 порядку (для задачі 4):

, , .

Умова стійкості явного методу Ейлера для системи ЗДР 1 порядку з постійними коефіцієнтами :

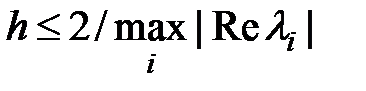, где , i =1, …, n, – власні числа матриці M порядку n.