Фрагмент РОЗВ’ЯЗКУ задачі 8.1.0

Многочлен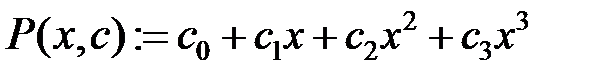

Коэффіціенти многочлена

Кінці відрізка інтегрування:

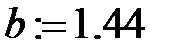
Значення інтегралу, обчислене аналітично:

Элементарна формула лівих прямокутників:

Абсолютна похибка:

Визначення максимуму мЗДРля похідної M1 многочлена на відрізку [a, b]:

Теоретична оцінка похибки

Складова формула левіх прямокутніків

Вичислення по складовою формулою левіх прямокутніків з Знайдені кроком h:

Контрольні питання

1.Найпростіші квадратурні формули (формули правих, лівих, центральних прямокутників, формула Трапецій, формула Сімпсона), геометрична ілюстрація, оцінки похибки. Точність квадратурних формул.

2.Квадратурні формули інтерполяційного типу: вивід формул, оцінки похибки.

3.Квадратурні формули Гаусса: вивід формул, точність формул.

4.Правило Рунге практичної оцінки похибки. Адаптивні процедури чисельного інтегрування.

5.Обчислити наближенно з кроком h=1 інтеграл по формулі:
a) правих прямокутників,
b) лівих прямокутників,
c) центральних прямокутників,
d) Трапецій,
e) Сімпсона.
Оцінити похибку на основі теоретичної оцінки похибки.

6.Впевнитись в тому, що формула центральних прямокутників точна для многочленів , а формула Сімпсона – для многочленів .

7.Оцінити теоретичне значення кроку інтегрування h для наближенного обчислення інтегралу по формулі Трапецій з точностю .

8.Оцінити теоретично значення кроку інтегрировання h для наближенного обчислення інтегралу по формулі Сімпсона з точностю .

9.Отримати квадратурні формули центральних прямокутників і Трапецій із загальної формули інтерполяційного типу.

10. Впевнитися в тому, що квадратурна формула Гаусса з одним вузлом точна для многочленів .

11. Обчислити наближено інтеграл по формулам Трапецій і Сімпсона з точністю , використовуючи правило Рунге практичної оцінки похибки.

12. Знайти оцінку похибки Обчислення інтегралу по составній формулі

13. Оцінити мінимальне число разиттів відрізка інтегрирування N для наближеного обчислення інтегралу по составній формулі Трапецій, яке забезпечує точність .

14. Побудувати квадратурні формули Чебишева на відрізку [-1,1] для обчислення для n=2,3,4.