Визначення вектора, дотичного до різальної кромки, в досліджуваній її точці

Схема обробки поверхні обертання круглим фасонним різцем (рис. 4.3.) включає швидке обертання заготовки (головний рух різання) і повільний прямолінійно-поступальний рух радіальної подачі різця. У момент формування поверхні деталі руху подачі вимикається і різальна кромка різця розташовується на обробленій поверхні деталі. З іншого боку різальна кромка лежить на передній поверхні. Як передня поверхня круглих фасонних різців, як правило, приймається площина. У загальному випадку в системі площин проекцій положення передньої площини круглого фасонного різця задається двома прямими, пересічними у вибраній базовій точці А різальної кромки. Однією прямою є пряма АЄ, розташована в площині перпендикулярної осі деталі. Другою прямою є горизонтальна пряма АВ. Положення прямої АЄ задається вибраною величиной інструментального переднього кута l_і. Положення горизонтальної прямої АВ визначається вибраною гвинтовою кута h.

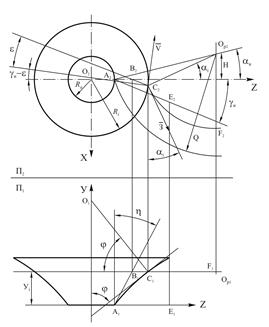
Рисунок 4.3

Найчастіше кут h приймається рівним і нулю. При обробці ж конічних поверхонь, з метою підвищення точності обробки, кут h приймається рівним половині кута при вершині конічної поверхні.

У системі xyz вектор Р₁, що йде по прямій АВ, буде:

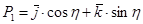. (4.85)

Вектор Р₂, що йде по прямій АЄ, буде:

. (4.86)

Вектор нормалі до передньої площини буде:

. (4.87)

Розкриваючи визначника отримаємо:

. (4.88)

У довільному перетині I, перпендикулярно осі деталі, точкою різальної кромки буде точка С. Вона визначається як точка перетину прямій ВС, що йде паралельно прямій АЄ, і кола радіусом R_i перерізу поверхні деталі і перетину I. Оскільки різальна кромка різця лежить на поверхні деталі, дотична до різальної кромки в точці Е лежатиме в площині дотичної в точці Е до поверхні деталі. Визначимо положення вектора нормалі`N<sub>S</sub> до поверхні деталі в точці С різальної кромки. Перетин I перетинається з поверхнею деталі по колу радіусом R<sub>i</sub>. Якщо в точках цього кола провести нормалі до поверхні деталі, то утворюється конус нормалей з вершиною в точці О. Лінія ОС буде нормаллю `N_S до поверхні деталі в точці С.

За побудовою матимемо:

, (4.89)

. (4.90)

де Rа – радіус базової точки різальної кромки;

Yi – координата "Y" точки С різальної кромки;

j - кут нахилу дотичної до заданого профілю деталі в перетині I.

Вектор `Р, що йде по дотичній до різальної кромки в досліджуваній точці `З буде:

. (4.91)

Розкриваючи визначника, після перетворень, отримаємо:

. (4.92)

Визначення статичних параметрів в нормальному до різальної кромки перетині

Вектор `V швидкості головного руху різання досліджуваної точки `З різальної кромки буде:

. (4.93)

Вектор нормали `N_p до поверхні різання

. (4.94)

Перетворюючи отримаємо:

. (4.95)

Статичний передній кут g_N в нормальному до різальної кромки перетині буде:

. (4.96)

Скалярний добуток векторов `N<sub>п</sub> та `N_р буде:

. (4.97)

Векторний добуток векторов буде:

. (4.98)

Розкриваючи визначник отримаємо:

. (4.99)

Модуль векторного добутку буде рівний:

. (4.100)

Таким чином

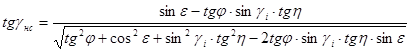. (4.101)

Найчастіше круглі фасонні різці проектуються при h=0 матимемо:

. (4.102)

Статичний задній кут a_нс в нормальному до різальної кромки перетині, поміщений між нормалью `N<sub>р</sub> до поверхні різання і нормалью `N_з до задньої поверхні в даній точці С різальної кромки. Кут a_нс між вектором `N<sub>р</sub> і вектором `N_з буде дорівнювати:

. (4.103)

Вектор `N_з нормалі до задньої поверхні буде:

. (4.103)

Вектор`З є вектором, який дотикається задньої поверхні інструменту.

Задня поверхня круглого фасонного різця є поверхнею обертання різальної кромки навколо осі О_р різця, яка йде паралельно осі деталі. Положення осі різця визначається радіусом Q різця в базовій точці А різальної кромки і прийнятою величиной інструментального заднього кута a_і в точці А. Підвищення Н осі різця над віссю деталі дорівнює:

. (4.104)

Точка С різальної кромки, обертаючись навколо осі різця, описує коло СF, розташоване на задній поверхні.

За побудовою задній кут в точці С в перетині перпендикулярному осі різця буде:

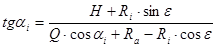. (4.105)

Вектор `З, дотичний до задньої поверхні в точки С буде:

. (4.106)

Вектор `N_з нормалі до задньої поверхні буде:

. (4.107)

Перетворюючи отримаємо:

. (4.108)

Скалярний добуток векторів `N<sub>р</sub> та `N_з буде:

. (4.109)

Модуль вектора `N_р буде:

. (4.110)

Модуль вектор `N_з буде:

. (4.111)

Таким чином:

.(4.112)

У випадку h=0 матимемо:

. (4.113)

При h=0 і j=0 матимемо

. (4.114)

Звідси a_нс=a_і+g_і-e.

Статичний кут нахилу різальної кромки l_с в досліджуваній її точці С визначається по залежності:

. (4.115)

Скалярний добуток векторів `V и `Р буде:

. (4.116)

Таким чином

. (4.117)

У випадку коли h=0 матимемо:

. (4.118)