Геометричні параметри круглих фасонних різців з похилою базою кріплення

4.4.1 Визначення вектора, дотичного до різальної кромки, в досліджуваній її точці

Схема обробки поверхні обертання круглим фасонним різцем з похилою базою кріплення включає швидке обертання заготовки навколо її осі (головний рух різання) і повільне прямолинейно- поступальний рух подачі. У момент формування поверхні деталі рух подачі вимикається і різальна кромка розташовується на обробленій поверхні деталі і є лінією перетину поверхні деталі і передньої площини. У системі площин проекцій П₁/П₃ (рис. 4.4) передня площина розташовується паралельно осі різця і йде перпендикулярно площини П₃. Положення передньої площини в системі П₁/П₃ визначається прийнятим значенням інструментального переднього кута g_і, вимірюваного в площині, перпендикулярній осі різця. Передня площина проходить через базову точку А різальної кромки. У системі площин проекцій П₁/П₂ положення передньої площини визначається двома прямими АВ і АЕ, положення яких визначається за правилом зміни площин проекцій, при відомому їх положенні в системі площин проекцій П₁/П₃.

За площину П₂ прийнята площина, перпендикулярна осі різця. Положення прямої А₂В₂ характеризується інструментальним переднім кутом g_іh. Відповідно до побудови передній кут g_іh рівний:

, (4.120)

де h - кут установки різця, ув’язнений між віссю різця і віссю деталі.

Рисунок4.4 – Геометричні параметри круглого фасонного різця з похилою базою кріплення.

Інструментальний передній кут g_іh вимірюється в перетині, перпендикулярному осі деталі.

У вибраному перетині I, перпендикулярному осі деталі, точкою різальної кромки буде точка С. Вона визначається як точка перетину прямої ЕС і кола радіусом R_i перерізу поверхні деталі і перетину I. Положення точки С визначається кутом d рівним:

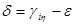. (4.121)

За побудовою матимемо:

, (4.122)

де R_a – радіус базової точки А поверхні деталі.

Величина Y=Y_i – відповідає положенню перетину I.

Вектор `N_S нормалі до поверхні деталі в точці С лежить на лінії ОС. Точка О є вершиною конуса нормалей, проведених до поверхні деталі в точках кола радіусу R_i, перерізу поверхні деталі і перетину I. Кут при вершині конуса нормалей буде 2j.

У системі xyz вектор нормалі `N_S до поверхні деталі в точці С буде:

. (4.123)

Паралельний вектор буде:

. (4.124)

У системі xyz вектор нормалі `N_П до передньої площини буде:

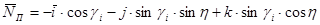. (4.125)

Вектор `Р, що йде по дотичною до різальної кромки буде:

. (4.126)

Розкриваючи визначника, отримаємо:

. (4.127)

Паралельний вектор буде:

. (4.128)

4.4.2 Визначення статичних геометричних параметрів в нормальному до різальної кромки перетині

Вектор `V швидкості головного руху різання в досліджуваній точці С різальної кромки буде:

. (4.129)

Вектор нормалі `N_p до поверхні різання буде:

. (4.130)

Паралельний вектор `N_p буде:

. (4.131)

Перетворюючи отримаємо:

. (4.132)

Вектор `N_П нормалі до передньої площини:

. (4.133)

Статичний передній кут g_Н в нормальному перетині:

. (4.134)

Скалярний добуток векторов `N<sub>p</sub> та `N_П буде:

, (4.135)

. (4.136)

Модуль вектора `N_П буде:

. (4.137)

Таким чином:

. (4.138)

Розглянемо окремий випадок, коли інструментальний передній кут g_i=0. Тоді матимемо: g₁=0; e=0; d=0. Вектор `Р дотичний до різальної кромки:

. (4.139)

Вектор швидкості головного руху різання: V=-i.

Вектор `N_p нормалі до поверхні різання:

. (4.140)

Вектор нормалі `N_П до передньої площини

. (4.141)

Таким чином передній кут g_нс буде рівний:

. (4.142)

Звідси g_нс=0.

Статичним кутом нахилу різальної кромки l_c в досліджуваній її точці С визначається по залежності:

. (4.143)

Скалярний добуток векторів `V та `Р буде:

. (4.144)

. (4.145)

Модуль вектора `V буде:

. (4.146)

Модуль вектора `Р буде:

. (4.147)

Таким чином:

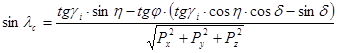. (4.148)

Розглянемо окремий випадок, коли інструментальний передній кут g_і=0. Тоді матимемо: d=0.

і l_с=0

Статичний задній кут в нормальному до різальної кромки перетині поміщений між нормалью `N<sub>p</sub> до поверхні різання і нормалью `N_з до задньої поверхні в даній точці різальної кромки.

Кут a_нс між вектором `N<sub>p</sub> і вектором `N_з рівний:

. (4.149)

Вектор нормалі до задньої поверхности `N_з буде дорівнювати:

. (4.150)

Вектор `З є вектором, який дотикається задньої поверхні інструменту. Задня поверхня круглого фасонного різця є поверхнею обертання різальної кромки навколо осі L різця, яка йде перпендикулярно площини проекцій П₃. Положення осі L різця визначається радіусом Q=А₃L₃ різця в базовій точці А різальної кромки і прийнятою величиной інструментального заднього кута a_іh в точці А. У даній точці С різальної кромки задній кут a_ih в перетині перпендикулярному осі різця поміщений між прямими L₃C₃ і C₃F₃. Аналізуючи графічне рішення матимемо:

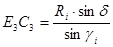, (4.151)

, (4.152)

, (4.153)

. (4.154)

де Q=А₃L₃ радіус різця в базовій точці А різальної кромки.

Вектор `З, дотичний кут задньої поверхні, в досліджуваній точці С різальної кромки, буде:

. (4.155)

Вектор нормали `N_з до задньої поверхні буде:

. (4.156)

Розкриваючи визначника, отримаємо:

. (4.157)

Скалярний добуток векторів `N<sub>p</sub> та `N_з буде:

, (4.158)

Отже:

. (4.159)