Маса системи. Центр мас

Рух системи залежить від її маси і від розподілу мас у системі.

Маса системи (позначається М або т) дорівнює арифметичній сумі мас всіх точок або тіл, що утворюють цю систему:

Розподіл мас у системі визначається значенням мас т_k і їх взаємним положенням, тобто координатами x_k, y_k, z_k. Не завжди при розв’язанні задач динаміки необхідні всі ці величини, потрібні тільки деякі, які виражаються через сумарні характеристики, а саме: координати центра мас, осьові моменти інерції. Ці характеристики ми розглянемо нижче.

Центр мас. Для визначення координат центра мас тіла дещо перетворимо відомі нам формули для визначення центра ваги тіла (див. лекц. №4), таким чином, щоб маса входила в явному вигляді. Для цього врахуємо, що , (g – прискорення вільного падіння), тоді:

, , .

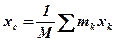Геометрична точка С, координати якої визначаються за цими формулами, називаються центром мас або центром інерції механічної системи.

Якщо положення центра мас визначається його радіусом-вектором , то маємо:

де 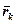– радіуси-вектори точок, які утворюють систему.

Звідси виходить, що для твердого тіла, яке знаходиться в однорідному полі тяжіння (g=const), положення центра мас і центра ваги збігаються.

3. Момент інерції тіла відносно осі. Радіус інерції

Моментом інерції тіла (системи) відносно даної осі Oz (або осьовим моментом інерції) називається скалярна величина, яка дорівнює сумі добутків мас всіх точок тіла (системи) на квадрати їх відстаней від цієї осі:

Звідси виходить, що момент інерції тіла (системи) відносно будь-якої осі є величиною додатною і відмінною від нуля. Одиницею вимірювання моменту інерції в системі СІ є 1 кг ּ м².

Момент інерції є мірою інертності тіла в обертальному русі, так само, як маса в поступальному.

При обчисленні осьових моментів інерції можна виражати відстані точок від осей через координати x_k, y_k, z_k цих точок (так, квадрат відстані від осі Ох буде і т.д.). Тоді моменти інерції відносно осей Oxyz будуть визначатися формулами:

,

,

.

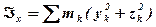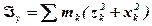Часто при розв’язанні задач доводиться користуватись поняттям радіуса інерції.

Радіусом інерції тіла відносно осі Oz називається лінійна величина ρ_z, яка визначається рівністю:

де M – маса тіла. Із означення виходить, що радіус інерції геометрично дорівнює відстані від осі Oz тієї точки, в якій необхідно зосередити масу всього тіла, щоб момент інерції цієї однієї точки дорівнював моменту інерції всього тіла.

Всі ці формули справедливі як для твердого тіла, так і для будь-якої системи матеріальних точок. У випадку суцільного тіла, розбиваючи його на елементарні частини, знайдемо, що гранично сума в рівності перетвориться в інтеграл. У результаті, враховуючи, що , де – густина, – об’єм, маємо:

або

або, враховуючи значення h², дістанемо:

і т.д..

Цими формулами зручно користуватись при обчисленні моментів інерції однорідних тіл правильної форми.

Наведемо формули для осьових моментів інерції деяких простих однорідних тіл.

1. Тонкий однорідний стержень довжиною l (рис.2).

Момент інерції відносно осі Az, перпендикулярної стержню, яка проходить через його кінець A:

2.Тонке кругле однорідне кільце (рис.3).

.

3. Кругла однорідна платівка (рис.3) або циліндр радіусом R (рис.4).

4.Однорідна куля (вісь z напрямлена вздовж діаметра).

5.Конус масою M з радіусом основи R (вісь z напрямлена вздовж осі конуса).

4. Момент інерції тіла відносно паралельних осей

Встановимо зв’язок між моментами інерції відносно паралельних осей, одна з яких проходить через центр мас системи. Вісь, яка проходить через центр мас тіла, називається центральною.

Оберемо початок прямокутної декартової системи координат в точці C – центрі мас системи (рис.2). У площині yCz проведемо вісь O'z', паралельну Cz і розміщенy на відстані d від неї. Позначимо: h_k– відстань k- ї матеріальної точки від осі z, h'_k– відстань цієї точки від осі z'.

Згідно означення:

Оскільки 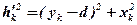, тоді:

Але оскільки .

Тоді маємо:

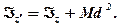
Рис.2

Момент інерції тіла відносно якої-небудь осі дорівнює її моменту інерції відносно центральної осі z, паралельної даній осі z', додатому до добутку маси системи на квадрат відстані між осями.

Із цієї рівності видно, що момент інерції відносно центральної осі найменший у порівнянні з усіма моментами інерції відносно паралельних їй осей.

Питання для самоконтролю

1.Що називається механічною системою?

2.Як класифікуються всі сили, що діють на систему? Їх означення.

3.Викласти властивості внутрішніх сил.

4.Як визначається маса системи, її центр мас?

5.Дати означення моменту інерції тіла відносно осі, навести формули його визначення через координати точок тіла.

6.Що називається радіусом інерції?

7.Як визначаються моменти інерції однорідних тіл: тонкого стержня, тонкого круглого кільця, круглої платівки або циліндра радіусом R, кулі, конуса?

8.Довести, як визначається момент інерції тіла відносно паралельних осей.

Лекція №30

Тема: “Теореми про зміну кількості руху точки та системи і теореми про зміну моменту кількості руху точки та системи”

План

1.Кількість руху матеріальної точки. Імпульс сили.

2.Теорема про зміну кількості руху точки.

3.Кількість руху системи.

4.Теорема про зміну кількості руху системи. Закон збереження кількості руху системи.

5.Теорема про зміну моменту кількості руху точки (теорема моментів).

6.Головний момент кількості руху системи.

7.Теорема про зміну головного моменту кількості руху системи (теорема моментів).

Для розв’язання багатьох задач динаміки (особливо в динаміці системи) замість безпосереднього інтегрування диференціальних рівнянь руху здається ефективнішим користуватись загальними теоремами, які є висновками основного закону динаміки.

Їх значення полягає у тому, що вони встановлюють наочні залежності між відповідними динамічними характеристиками тіл. Крім того, застосування теорем позбавляє необхідності інтегрувати і цим самим спрощує процес розв’язання задачі.

Перейдемо до розгляду загальних теорем динаміки.

1. Кількість руху матеріальної точки. Імпульс сили

Кількість руху – одна із основних динамічних характеристик руху точки.

Кількістю руху матеріальної точки називається векторна величина , яка дорівнює добутку маси точки на її швидкість. Цей вектор напрямлений так само, як і швидкість точки, тобто по дотичній до її траєкторії. Одиниця вимірювання в системі СІ – 1 кг ּ м/с =1 Н ּ с.

Для характеристики дії сили на тіло за деякий проміжок часу вводиться поняття імпульсу сили.

Елементарним імпульсом сили називається векторна величина , яка дорівнює добутку сили на елементарний проміжок часу dt:

Напрямлений елементарний імпульс вздовж лінії дії сили.

Імпульс будь-якої сили за кінцевий проміжок часу 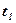дорівнює:

.

Отже, імпульс сили за деякий кінцевий проміжок часу 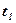дорівнює визначеному інтегралу від елементарного імпульсу, взятому від нуля до .

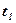Зокрема, якщо – величина стала ( =const), то:

У загальному випадку модуль імпульсу може бути обчислений за його проекціями на координатні осі:

Одиницею вимірювання імпульсу в системі СІ є 1 кг ּ м/с = 1 Н ּ с, тобто така, як і кількості руху.

2. Теорема про зміну кількості руху точки

Оскільки , то основний закон динаміки можна записати у вигляді:

Це рівняння виражає одночасно теорему про зміну кількості руху в диференціальній формі: похідна від кількості руху точки за часом дорівнює геометричній сумі всіх сил, що діють на точку.

Нехай точка має в момент часу t=0 швидкість , а в момент 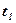– швидкість . Помножимо обидві частини рівності на dt і візьмемо інтеграл:

Праворуч інтеграли є імпульсами сил. Тому остаточно:

Це рівняння виражає теорему про зміну кількості руху точки в кінцевому вигляді: зміна кількості руху точки за деякий проміжок часу дорівнює сумі імпульсів всіх сил, що діють на точку, за той же проміжок часу.

При розв'язанні задач замість векторного рівняння часто користуються рівняннями в проекціях:

3. Кількість руху системи

Кількістю руху системи будемо називати векторну величину , яка дорівнює геометричній сумі (головному вектору) кількості руху всіх точок системи (рис.1):

Рис.1

Із рівності (див. лекц.№29) виходить, що:

Беручи із обох частин похідну за часом, дістанемо:

або

звідси:

Тобто, кількість руху системи дорівнює добутку маси всієї системи на швидкість її центра мас.

Із формули бачимо, що якщо тіло (або система) рухається так, що центр мас її залишається нерухомим, то кількість руху тіла дорівнює нулю. Наприклад, тіло, яке обертається навколо нерухомої осі, що проходить через його центр мас. Якщо ж рух тіла є складним, то величина не залежить від обертального руху навколо центра мас.

4. Теорема про зміну кількості руху системи. Закон збереження кількості руху системи

Нехай система складається із n матеріальних точок. Тоді дістанемо:

Остання сума за властивостями внутрішніх сил дорівнює нулю. Крім цього:

Остаточно маємо:

Це рівняння виражає теорему про зміну кількості руху системи в диференціальній формі: похідна за часом від кількості руху системи дорівнює геометричній сумі всіх зовнішніх сил, що діють на систему.

У проекціях на координатні осі маємо:

Нехай у момент часу t=0 кількість руху системи дорівнювала , а в момент . Тоді після інтегрування дістанемо:

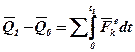
або

Це рівняння виражає теорему про зміну кількості руху системи в інтегральній формі: зміна кількості руху системи за деякий проміжок часу дорівнює сумі імпульсів всіх зовнішніх сил, що діють на систему, за той же проміжок часу.

У проекціях на координатні осі будемо мати:

Із теореми про зміну кількості руху системи можна зробити висновки:

1. Якщо сума всіх зовнішніх сил, що діють на систему, дорівнює нулю:

тоді =const. Отже, якщо сума всіх зовнішніх сил, які діють на систему, дорівнює нулю, то вектор кількості руху системи буде сталим за модулем і напрямком.

2. Якщо зовнішні сили, що діють на систему, такі, що сума їх проекцій на яку-небудь вісь (наприклад Oх) дорівнює нулю:

тоді Q_x=const. Таким чином, якщо сума проекцій всіх зовнішніх сил, які діють на систему, на яку-небудь вісь дорівнює нулю, то проекція кількості руху системи на цю вісь є величиною сталою.

Ці результати і виражають закон збереження кількості руху системи.

5. Теорема про зміну моменту кількості руху точки (теорема моментів)

У деяких задачах замість кількості руху розглядають її момент відносно деякого центра або осі.

Ці моменти визначаються так само, як і моменти сили.

Таким чином, моментом кількості руху точки відносно деякого центра О називається векторна величина , яка визначається рівністю:

де – радіус-вектор точки, проведений із центра О.

Момент напрямлений перпендикулярно площині, яка проходить через і центр О, а (рис.2).

Момент кількості руху точки відносно якої-небудь осі Oz, яка проходить через центр О, буде дорівнювати проекції вектора на цю вісь:

де γ – кут між вектором і віссю Oz.

Теорема моментів встановлює, як змінюється з часом . Щоб її довести, продиференціюємо за часом вираз дістанемо:

Але , як векторний добуток двох паралельних векторів, а 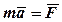, або при дії декількох сил , тоді:

або

Отже, ми довели теорему моментів відносно центра: похідна за часом від моменту кількості руху точки, взятого відносно якого-небудь нерухомого центра, дорівнює моменту сили, що діє на точку, відносно того ж центра.

Якщо спроектувати обидві частини останнього рівняння на яку-небудь вісь Oz, яка проходить через центр О, то дістанемо:

Це рівняння виражає теорему моментів відносно осі.

Якщо , то , тобто якщо момент сили відносно деякого центра дорівнює нулю, то момент кількості руху точки відносно цього центра є величиною сталою.

6. Головний момент кількості руху системи

Головним моментом кількості руху (або кінетичним моментом) системи відносно даного центра О називається величина , яка дорівнює геометричній сумі моментів кількості руху всіх точок системи відносно цього центра:

Аналогічно визначаються моменти кількості руху системи відносно координатних осей:

При цьому K_x, K_y i K_z ‑ проекції вектора на координатні осі.

Головний момент кількості руху (кінетичний момент) системи може розглядатися як характеристика її обертального руху.

Якщо тіло обертається навколо осі з кутовою швидкістю ω, то швидкість точки, розміщеної на відстані h_k від осі обертання, дорівнює , тоді для неї або

Величина в дужках є не що інше, як момент інерції тіла відносно осі z. Остаточно:

Таким чином, кінетичний момент тіла, яке обертається, відносно осі обертання дорівнює добутку моменту інерції тіла відносно цієї осі на кутову швидкість тіла.

Ця формула справедлива і для повороту тіла навколо миттьової осі обертання з кутовою швидкістю ω, отже:

7. Теорема про зміну головного моменту кількості руху системи(теорема моментів)

Теорема моментів, доведена для однієї матеріальної точки, справедлива для кожної точки системи.

Якщо розглянути точку системи масою m_k, яка має швидкість , то будемо мати:

де і – рівнодійні всіх зовнішніх i внутрішніх сил.

Для всіх точок системи:

Остання сума за властивостями внутрішніх сил дорівнює нулю. Тоді:

Ця рівність виражає теорему моментів системи: похідна за часом від головного моменту кількості руху системи відносно деякого нерухомого центра дорівнює сумі моментів всіх зовнішніх сил системи відносно цього ж центра.

Проектуючи обидві частини рівності на нерухомі осі Oxyz, дістанемо:

Розглянуті вище теореми мають важливе значення. У кінематиці було показано, що рух твердого тіла в загальному випадку складається із поступального руху разом з полюсом і обертального навколо нього. Якщо за полюс взяти центр мас, то поступальна частина руху тіла може бути вивчена за допомогою теореми про зміну кількості руху (про рух центра мас), а обертальна – за допомогою теореми моментів.

Питання для самоконтролю

1. Що називається кількістю руху матеріальної точки? Одиниці її вимірювання.

2. Дати означення елементарному імпульсу сили.

3. Чому дорівнює імпульс сили за кінцевий проміжок часу? У випадку = const?

4. Сформулювати та довести теорему про зміну кількості руху матеріальної точки.

5. Що називається кількістю руху системи?

6. Вивести формулу визначення кількості руху системи.

7. Сформулювати і довести теорему про зміну кількості руху системи.

8. Викласти закон збереження кількості руху системи.

9. Дати означення моменту кількості руху точки відносно центра та осі.

10. Сформулювати і довести теорему про зміну моменту кількості руху точки відносно центра та осі.

11. Як визначається кінетичний момент системи відносно центра та осі?

12. Сформулювати та довести теорему про зміну кінетичного моменту системи.

Лекція № 31

Тема: “Теореми про зміну кінетичної енергії матеріальної точки і системи”

План

1.Робота сили. Потужність.

2.Теорема про зміну кінетичної енергії матеріальної точки.

3.Кінетична енергія системи.

4.Теорема про зміну кінетичної енергії системи.

1. Робота сили. Потужність

Для характеристики дії сили на тіло на деякому його переміщенні вводиться поняття роботи сили. Спочатку скажемо про елементарну роботу.

Елементарною роботою сили , прикладеної в точці М (рис.1), називається скалярна величина, що дорівнює:

де F_τ – проекції сили на дотичну Mτ до траєкторії точки М, напрямлену в бік переміщення цієї точки (або проекція на напрямок швидкості точки М); ds – модуль елементарного переміщення точки М

Якщо розкласти силу на складові і , то змінювати модуль швидкості буде , оскільки (складова змінює напрямок вектора швидкості ).

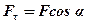Із рис.1 бачимо, що , де α – кут між і Mτ. Тоді дістанемо, що

Якщо кут α гострий, то робота додатна, якщо α=0, то .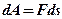

Якщо кут α тупий, то робота від'ємна. При α=180⁰ .

Якщо α=90⁰, тобто якщо сила напрямлена перпендикулярно переміщенню, то елементарна робота сили дорівнює нулю.

Знак роботи містить у собі такий зміст: робота додатна, коли складова напрямлена в бік руху (сила прискорює руху); робота від'ємна, коли складова напрямлена в бік, протилежний руху (сила сповільнює рух).

Якщо врахувати, що , де – вектор елементарного переміщення точки, то:

.

Отже, елементарна робота сили дорівнює скалярному добутку сили на вектор елементарного переміщення точки її прикладання.

Виразимо скалярний добуток через проекції на координатні осі:

де x, y, z – координати точки прикладання сили .

Робота сили на будь-якому кінцевому переміщенні M₀M₁ (рис.1) обчислюється як границя інтегральної суми відповідних елементарних робіт:

або

Отже, робота сили на будь-якому переміщенні M₀M₁ дорівнює взятому вздовж цього переміщення інтегралу від елементарної роботи.

Якщо сила стала ( = const), то, позначаючи M₀M₁ через s₁, дістанемо:

Зокрема, якщо сила стала за модулем і напрямком ( =const), а точка, до якої прикладена сила, рухається прямолінійно (рис.2), то в цьому випадку: , а

Одиницею вимірювання роботи в системі СІ є 1Джоуль (1Дж = 1Н ּ м= 1кг ּ м²/с²).

Потужність. Потужністю називається величина, яка визначає роботу, що здійснює сила за одиницю часу. Якщо робота виконується рівномірно, то

де t₁ – час, за який виконана робота A.

У загальному випадку:

Отже, потужність дорівнює добутку дотичної складової сили на швидкість.

Одиницею вимірювання потужності в системі СІ є 1Ват (1Вт = 1Дж/с). У техніці за одиницю потужності часто вживають кінську силу (1к.с.), яка дорівнює 736Вт.

Роботу, виконану машиною, можна вимірювати добутком її потужності на час роботи. Звідси 1кіловат-година (1кВт ּ г = 3,6 ּ 10⁶Дж).

Із рівності N=F_τv видно, що у двигуна, який має певну потужність, сила тяги F_τ буде тим більшою, чим менша швидкість v.

2. Теорема про зміну кінетичної енергії матеріальної точки

Другою основною динамічною характеристикою руху точки є кінетична енергія.

Кінетичною енергією матеріальної точки називається скалярна величина , яка дорівнює половині добутку маси точки на квадрат її швидкості.

Одиниця вимірювання її та ж, що й роботи, тобто в системі СІ – 1Дж. Визначимо залежність між цими величинами.

Нехай матеріальна точка масою m переміщається із положення М₀, де вона мала швидкість v₀, в положення M₁, де її швидкість v₁.

Запишемо залежність, яка виражає основний закон динаміки:

Проектуючи її на дотичну Mτ до траєкторії точки M, напрямлену в бік руху, дістанемо:

Дотичне прискорення подамо у вигляді:

У результаті:

Помножимо обидві частини рівняння на ds і занесемо m під знак диференціалу. Тоді F_kτds=dA_k, де dA_k – елементарна робота сили . У результаті дістанемо вираз для теореми про зміну кінетичної енергії точки в диференціальній формі:

Проінтегрувавши обидві частини цієї рівності в межах, які відповідають значенням змінних М₀ і M₁, остаточно знайдемо:

Це рівняння виражає теорему про зміну кінетичної енергії точки в кінцевому вигляді: зміна кінетичної енергії точки на деякому її переміщенні дорівнює алгебраїчній сумі робіт всіх сил, що діють на точку, на тому ж переміщенні.

Теорема дає можливість, знаючи як в процесі руху точки змінюється її швидкість, визначити роботу сил (перша задача) або, знаючи роботу сил, що діють на точку, визначити, як змінюється у процесі руху швидкість точки (друга задача динаміки).

3. Кінетична енергія системи

Кінетичною енергією системи називається величина Т, яка дорівнює сумі кінетичних енергій всіх точок системи:

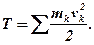
Кінетична енергія є характеристикою і поступального, і обертального руху системи.

Кінетична енергія Т – величина скалярна на відміну від кількості руху і кінетичного моменту відносно центра . Відмінною рисою Т є і те, що на її зміну впливає дія внутрішніх і зовнішніх сил.

Розглянемо, як визначається кінетична енергія тіла в різних випадках руху.

1. Поступальний рух. У цьому випадку всі точки рухаються з однаковими швидкостями, які дорівнюють швидкості центра мас. Отже, v_k=v_c, тоді:

або

Таким чином, кінетична енергія тіла у поступальному русі дорівнює половині добутку маси тіла на квадрат швидкості його центра мас.

2. Обертальний рух. Якщо тіло обертається навколо осі Oz, то швидкість будь-якої його точки v_k=ωh_k, де h_k – відстань точки від осі обертання, а ω – кутова швидкість тіла. Підставляючи значення в формулу і виносячи спільні множники за дужки, дістанемо:

Величина в дужках є моментом інерції тіла відносно осі z. Таким чином,

Кінетична енергія тіла у обертальному русі дорівнює половині добутку моменту інерції тіла відносно осі обертання на квадрат його кутової швидкості.

3. Плоскопаралельний рух. Плоскопаралельний рух тіла можна подати як обертальний рух навколо миттьового центра швидкостей Р (рис.3). Тоді,

де – момент інерції тіла відносно осі, яка проходить через миттьовий центр швидкостей; ω – кутова швидкість обертання тіла.

Величина – змінна, оскільки положення центра Р у процесі руху весь час змінюється. Визначимо цей момент інерції як:

де d=PC.

Оскільки Р – миттьовий центр швидкостей, то ωd=ω PC=v_c, де v_c – швидкість центра мас С (рис.3), остаточно:

Отже, у плоскопаралельному русі кінетична енергія тіла дорівнює енергії поступального руху зі швидкістю центра мас та енергії обертального руху навколо центра мас.

4. Теорема про зміну кінетичної енергії системи

Теорема про зміну кінетичної енергії матеріальної точки справедлива для будь-якої точки системи. Отже, якщо розглянути довільну точку системи масою m_k, яка має швидкість v_k, то:

де і – елементарні роботи зовнішніх і внутрішніх сил, що діють на точку. Або для всіх точок системи:

або

Ця рівність виражає теорему про зміну кінетичної енергії системи в диференціальній формі.

Проінтегрувавши обидві частини рівності в границях, які відповідають переміщенню системи із початкового положення, де кінетична енергія дорівнювала T₀, у положення, де значення кінетичної енергії дорівнює T₁, дістанемо:

Ця рівність виражає теорему про зміну кінетичної енергії системи в інтегральній формі: зміна кінетичної енергії системи на деякому її переміщенні дорівнює сумі робіт на цьому переміщенні всіх зовнішніх і внутрішніх сил, прикладених до системи.

Внутрішні сили тут залишаються. Так, нехай і – сили взаємодії між точками В₁ і В₂, тоді (рис. 4). Але при цьому точка В₁ може переміщатись у напрямку до В₂, а В₂ – у напрямку до В₁. Тоді робота кожної сили буде додатна, і сума їх робіт не дорівнюватиме нулю.

Тільки у випадку незмінної системи будемо мати, що сума робіт всіх внутрішніх сил дорівнює нулю, тоді:

або

Незмінними системами називають такі, у яких відстань між кожними двома її точками за весь час руху залишається сталою.

Питання для самоконтролю

1.Дати означення елементарній роботі. Формула визначення та її аналіз.

2.Як визначається робота на кінцевому переміщенні точки?

3. Що таке потужність? За якою формулою вона визначається? Одиниці її вимірювання.

4.Що називається кінетичною енергією точки? Одиниці її вимірювання.

5.Сформулювати і довести теорему про зміну кінетичної енергії точки.

6.Як визначається кінетична енергія поступального, обертального і плоскопаралельного рухів тіла?

7.Сформулювати і довести теорему про зміну кінетичної енергії системи.

Лекція №32

Тема: “Теорема про рух центра мас. Застосування загальних теорем динаміки до руху твердого тіла”

План

1.Диференціальні рівняння руху системи.