Теорема про додавання прискорень 6 страница

Якщо ж тепер цю точку А віднести до веденої вилки 3, то колова швидкість буде:

де – кутова швидкість веденої вилки 3; AС – перпендикуляр, опущений із точки А на вісь обертання веденої вилки 3.

Але:

Отже:

або

.

Звідси:

Якщо повернемо універсальний шарнір на кут 90°, то:

.

Таким чином, в універсальному шарнірі при сталій кутовій швидкості ведучої вилки 1 ведена вилка 3 обертається нерівномірно, причому передаточне відношення змінюється в межах від cosα до .

Середня кутова швидкість ω_3ср веденої вилки 3 дорівнює сталій кутовій швидкості ω₁ ведучої вилки 1, оскільки за час одного оберту вилки 1 вилка 3 також здійснить один оберт.

2. Карданні передачі

Зв’язок між валом відбору потужності трактора і приймальним валом сільськогосподарської машини здійснюється за допомогою карданної передачі.

Карданна передача складається із декількох валів, з’єднаних універсальними шарнірами. Бувають дво-, три- і чотиришарнірні карданні передачі.

Найпоширенішою карданною передачею є тришарнірна (рис.2). Вона складається із вала відбору потужності 1, телескопічного вала 2, проміжного вала 3, запобіжної муфти 4, приймального вала сільськогосподарської машини 5, універсальних шарнірів А, В і С.

Рис.2

Телескопічне з’єднання валів виконується у вигляді рухомого шліцьового з’єднання (або квадратного вала та труби з квадратним отвором) і забезпечує осьове переміщення валів карданної передачі при пересуванні сільськогосподарської машини по нерівному полю та на поворотах.

3. Механізми передач з гнучкими ланками

До механізмів передач з гнучкими ланками відносяться передачі:пасова;канатна;ланцюгова тощо.

До переваг пасових передач належать:

- можливість передачі рухів на відстані;

- плавність і безшумність роботи;

- запобігання перевантаженню механізмів за рахунок проковзування пасів;

- можливість роботи з високими швидкостями;

- невисока вартість.

Їх недоліками є:

- значні габарити;

- необхідність пристроїв для натягування паса у передачах з малою міжосьовою відстанню;

- мала довговічність пасів у швидкохідних передачах;

- неминучість деякого пружного ковзання паса.

Передачі з гнучкими ланками широко застосовуються у вигляді ланцюгових передач, в яких зубчаті зірочки входять у зачеплення із ланками ланцюга. Такі механізми застосовують у сільськогосподарських машинах, транспортерах, гірничих машинах тощо.

Ланцюгові передачі в порівнянні з пасовими відрізняються:

- відсутністю ковзання;

- високим коефіцієнтом корисної дії;

- меншими габаритами.

Але в той же час вони працюють в умовах відсутності рідинного тертя і, як наслідок, з неминучим спрацюванням, а також потребують більш високої точності установки валів, ніж клинопасові. До того ж швидкість руху ланцюга, особливо при малій кількості зубів зірочок, не стала, що викликає нерівномірність обертання зірочок.

При передачі руху гнучкою ланкою за допомогою круглих шківів (рис.3) передаточне відношення дорівнює:

,

тобто передаточне відношення дорівнює оберненому відношенню радіусів R₁ і R₃ шківів 1 і 3.

Рис.3.

Механізм передачі з гнучкою ланкою, зображений на рис.3, носить назву відкритої передачі, а на рис.4 – перехресної. Передаточне відношення останньої визначається:

.

Рис.4.

Механізми передач з гнучкими ланками досить глибоко розглядаються в модулі “Розрахунок вузлів та деталей машин” курсу технічної механіки.

4. Загальні відомості про хвильові передачі

Розглянемо конструкцію хвильової передачі, зображеної на рис.5.

Так само, як і планетарна, хвильова передача складається з трьох основних ланок: 1 – генератор хвиль, який виконаний у вигляді водила з двома роликами; 2 – гнучке колесо – пружна тонкостінна склянка, основа якої з’єднана з веденим валом, а на потовщеному вінці поблизу торця нарізані зубці; 3 – нерухоме жорстке колесо з внутрішніми зубцями.

Рис.5

Модулі зачеплення коліс 2 і 3 однакові, а кількість зубів гнучкого колеса 2 менша, ніж колеса 3 (z₂<z₃). Різниця z₃-z₁=W характеризує кількість хвиль деформації гнучкого колеса. Оптимальне значення W=2.

Ділильні діаметри теж неоднакові: d₃>d₂. У вільному стані (без генератора) колеса розміщені концентрично з рівномірним зазором між зубцями. При встановленому генераторі останній деформує гнучке колесо в радіальному напрямку, надаючи йому форму еліпса: по великій осі еліпса (зона А) зубці зачіпляються на повну робочу висоту, а по малій осі (зона В) – між вершинами зубів утворюється радіальний зазор, а в зоні С зачеплення проміжне.

У процесі обертання генератора форма гнучкого колеса залишається близькою до описаної і лише змінює свої координати, тобто зачеплення зубів переміщається синхронно з роликами, подібно біжучій хвилі, – звідси назва хвильових передач.

Передаточне відношення хвильової передачі позначається так само, як і зубчатої планетарної, – літерою u з індексами: верхній вказує на нерухому ланку, два нижні – на ланки, які обертаються:

Знак “мінус” вказує на те, що ведуча і ведена ланки обертаються в протилежних напрямках.

В одноступінчатих зубчатих хвильових редукторах діапазон и=50÷1000.

У хвильових передачах знаходиться в зачепленні одночасно 25-30% пар зубів.

Питання для самоконтролю

1. Призначення універсального шарніра (шарніра Гука), його будова та принцип роботи.

2. Як визначається передаточне відношення універсального шарніра?

3. Призначення карданної передачі, її будова.

4. Перелічіть механізми передач з гнучкими ланками. Як визначається їх передаточне відношення?

5. Описати будову хвильової передачі.

6. Принцип роботи хвильової передачі. Її передаточне відношення.

МОДУЛЬ „ДИНАМІКА”

ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ ТА МЕХАНІЧНОЇ СИСТЕМИ

Лекція №26

Тема: “Закони динаміки. Диференціальні рівняння руху матеріальної точки. Розв’язання першої задачі динаміки”

План

1.Закони динаміки.

2.Диференціальні рівняння руху матеріальної точки.

3.Дві задачі динаміки. Розв’язання першої задачі.

1.Закони динаміки

Динамікою називається розділ механіки, в якому рух матеріальних тіл вивчається з урахуванням сил, що діють на них.

Поняття сили, як основної міри механічної дії, було введено в статиці.

Для механіки важливою властивістю тіла є його інертність, яка виявляється в тому, що тіло зберігає свій рух при відсутності сил. Кількісною мірою інертності матеріального тіла є фізична величина, яка називається масою тіла. У класичній механіці маса m розглядається як величина скалярна, додатна і стала для кожного даного тіла.

Основою динаміки є закони Ньютона.

Перший закон(закон інерції): ізольована від зовнішньої дії матеріальна точка зберігає свій стан спокою або рівномірного прямолінійного руху до тих пір, поки прикладені сили не вимусять її змінити цей стан. Рух, який здійснює точка при відсутності сил, називається рухом по інерції.

Система відліку, відносно якої справедливий цей закон, називається інерціальною системою відліку. При розв’язанні багатьох задач механіки систему координат, жорстко зв’язану з Землею, можна вважати інерціальною.

Ізольованою називається така матеріальна точка, яка не взаємодіє з іншими матеріальними тілами або якщо її взаємодією з іншими тілами можна знехтувати.

Другий (основний) закон: добуток маси матеріальної точки на прискорення, яке вона дістає внаслідок дії сили, дорівнює модулю цієї сили, а напрямок прискорення збігається з напрямком сили.

Цей закон виражається рівністю:

.

Другий закон, як і перший, має місце тільки по відношенню до інерціальної системи відліку.

Якщо на точку діють одночасно декілька сил, то вони будуть еквівалентні одній силі, тобто рівнодійній , яка дорівнює геометричній сумі цих сил. Тоді рівняння набуде вигляду:

або .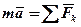

Третій закон (закон рівності дії і протидії): дві матеріальні точки діють одна на одну з силами, однаковими за модулем і напрямленими вздовж прямої, яка з’єднує ці точки, в протилежні боки.

Цей закон (аксіома) розглядався нами в статиці. Нагадаємо, що сили взаємодії в загальному випадку не є зрівноваженими, бо вони прикладені до різних точок. Тільки для твердого тіла сили взаємодії між його точками можна вважати зрівноваженими. На відміну від першого і другого законів динаміки, третій справедливий у будь-якій системі відліку, тому що він не містить кінематичних параметрів руху точки.

Сформулюємо принцип незалежності дії сил (принцип суперпозиції), який застосовується у процесі розв’язання деяких задач механіки: прискорення матеріальної точки, яке виникає внаслідок одночасної дії на неї декількох сил, дорівнює геометричній сумі прискорень, які надає точці кожна сила окремо:

,

де .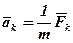

Застосування цього принципу еквівалентно заміні сил, що діють на матеріальну точку, їх рівнодійною. Але цей принцип справедливий не завжди. Він, зокрема, не має місця, якщо сили, що діють на точку, залежать від її прискорення.

2. Диференціальні рівняння руху матеріальної точки

У кінематиці розглядаються три способи задання руху точки: векторний, координатний і натуральний. У зв’язку з цим, базуючись на другому законі динаміки, виводяться диференціальні рівняння руху матеріальної точки в трьох формах: векторній, координатній та натуральній.

Рівняння у векторній формі. Із кінематики відомо, що рівняння руху точки у векторній формі має вигляд:

,

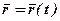де – радіус-вектор, який визначає положення точки в будь-який момент часу.

Прискорення точки дорівнює:

Підставляючи це значення у формулу для визначення сили, маємо:

.

Ця рівність називається диференціальним рівнянням руху матеріальної точки у векторній формі. Якщо на точку діє декілька сил, то:

Рівняння в координатній формі. Рух точки в прямокутних декартових координатах задається рівняннями:

Знайдемо рівняння, які пов’язують координати x, y, z цієї точки і силу (або сили), що діє на неї. Ці рівняння дає другий закон динаміки.

Розглянемо матеріальну точку, яка рухається під дією сил , ,..., по відношенню до інерціальної системи відліку Oxyz. Проектуючи обидві частини рівності на осі x, y, z і враховуючи, що , та , дістаємо:

або, позначаючи другі похідні за часом двома штрихами, маємо:

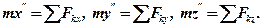
Це і є диференціальні рівняння руху точки в прямокутних декартових координатах.

Оскільки діючі на точку сили можуть залежати від часу t, від координат x, y, z і від швидкості, тобто v_x=x', v_y=y', v_z=z', то в загальному випадку права частина кожного рівняння може бути функцією всіх цих змінних, тобто, t, x, y, z, x', y', z' одночасно.

Рівняння в натуральній формі. Для того щоб дістати ці рівняння, спроектуємо обидві частини рівності на осі натурального тригранника Мτnb, тобто на дотичну Мτ до траєкторії точки, головну нормаль Мn, напрямлену в бік угнутості траєкторії, і бінормаль Мb. Тоді, враховуючи, що:

дістаємо:

Ці рівняння, де , є диференціальними рівняннями руху точки в натуральній формі.

3. Дві задачі динаміки. Розв’язання першої задачі

На основі диференціальних рівнянь матеріальної точки можна розв’язати такі основні задачі її динаміки:

1) перша задача (пряма): визначення величини і напрямку сили, яка діє на точку, знаючи масу точки і закон її руху;

2) друга задача (обернена, основна): знаходження закону руху точки, якщо відомі маса точки і сили, що діють на неї.

Розглянемо загальну методику розв’язання першої задачі динаміки точки. Воно здійснюється у такій послідовності:

1) диференціювання двічі за часом функцій, які виражають кінематичний закон руху точки;

2)підставлення результатів диференціювання у відповідні диференціальні рівняння й отримання з них значень проекцій сил;

3) визначення модуля сили і косинусів кутів, які визначають напрямок сили (за формулами, відомими із векторної алгебри).

Якщо рух матеріальної точки заданий у координатній формі, тобто задані: диференціюємо двічі ці функції за часом. Дістаємо проекції a_x, a_y, a_z прискорення точки на координатній осі:

Підставляючи ці значення в рівняння для визначення сили, маємо:

Далі за формулами:

визначимо модуль і напрямні косинуси вектора сили.

Якщо рух матеріальної точки заданий натуральним способом, тобто задані траєкторія точки і закон s=s(t) її руху, то диференціюючи за часом функцію s=s(t), знайдемо алгебраїчне значення швидкості точки . Далі за формулою визначимо значення дотичного прискорення, а за формулою – нормального. Підставляючи значення m, a_τ i a_n у формули, дістанемо значення проекцій сили на дотичну і головну нормаль:

Зрештою, за формулами:

визначимо модуль сили і значення кута між головною нормаллю та напрямком сили.

Задача. Матеріальна точка, що має масу m =4 г, рухається згідно рівнянь:

x=3sin t, y=cos t, (x, y – в см, t – в с).

Визначити модуль і напрямок вектора сили, яка діє на точку.

Розв’язання. Оскільки рівняння руху точки задані координатним способом, то проекції сили визначаємо за формулами:

Диференціюючи двічі за часом задані функції, дістанемо:

Тоді:

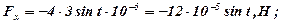
Остаточно:

Питання для самоконтролю

1.Що вивчає розділ “Динаміка”?

2.Сформулювати три закони динаміки (Ньютона).

3.Вивести диференціальні рівняння руху матеріальної точки у трьох формах: векторній, координатній та натуральній.

4.Сформулювати дві задачі динаміки.

5.Яка послідовність розв’язання першої задачі динаміки?

6.Розв’язання першої задачі динаміки при координатному способі задання руху точки.

7.Розв’язання першої задачі динаміки при натуральному способі задання руху точки.

Лекція №27

Тема: “Розв’язання другої задачі динаміки точки”

План

1.Загальна методика розв’язання другої задачі динаміки точки.

2.Розв’язання другої задачі динаміки при прямолінійному русі точки.

3.Розв’язання другої задачі динаміки при криволінійному русі точки.

1.Загальна методика розв’язання другої задачі динаміки точки

Нагадаємо, що друга задача динаміки точки полягає в тому, щоб, знаючи силу, яка діє на точку, знайти кінематичний закон її руху. Розв’язання цієї задачі зводиться до інтегрування диференціальних рівнянь руху матеріальної точки при заданих початкових умовах і виконується в такій послідовності:

1) складання диференціальних рівнянь руху точки, виходячи із умови задачі;

2) знаходження загальних розв’язків складених рівнянь;

3) визначення значень сталих інтегрування за заданими початковими умовами руху точки;

4) отримання кінематичних рівнянь, які виражають закон руху точки, шляхом підставлення сталих інтегрування в загальні розв’язки.

У попередній лекції показано, як на основі другого закону динаміки складаються диференціальні рівняння руху точки. При цьому в залежності від способу задання руху точки рівняння можуть бути складені в трьох формах – векторній, координатній і натуральній.

При складанні диференціальних рівнянь руху матеріальної точки в координатній формі слід обрати систему координат Oxyz (початок її, як правило, суміщають з початковим положенням точки), зобразити на рисунку точку в довільному положенні так, щоб її координати і проекції швидкості були додатними Далі необхідно зобразити силу (сили), які діють на точку в даний момент часу. Після цього скласти диференціальні рівняння руху точки в проекціях на осі обраної системи координат. При цьому змінні сили повинні бути подані в рівняннях в явному вигляді як функції відповідних аргументів.

Нагадаємо, що диференціальні рівняння руху точки, на яку діє сила, що залежить від часу, положення точки і її швидкості, мають вигляд:

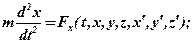
де

Отже, отримання кінематичних рівнянь x=x(t), y=y(t), z=z(t), які виражають закон руху точки, зводиться до інтегрування цих диференціальних рівнянь. Щоб задача динаміки була визначеною, необхідно крім сили, що діє на точку, задати початкові умови руху точки. Це значить для деякого моменту часу t=t₀ задати значення функцій і їх похідних. Початкові умови записуються у вигляді:

Відзначимо, що початкові умови руху матеріальної точки містяться в самій постановці задачі динаміки і мають певний механічний зміст. Введенням початкової швидкості враховується вплив всіх раніше діючих на точку сил та подальший її рух.

2.Розв’язання другої задачі динаміки при прямолінійному русі точки

Рух матеріальної точки буде прямолінійним, якщо сила (або рівнодійна прикладених сил), яка діє на неї, буде сталою за напрямком, а швидкість точки в початковий момент часу дорівнює нулю або напрямлена вздовж лінії дії сили.

Нехай матеріальна точка рухається прямолінійно. На точку вздовж траєкторії її руху діє сила , яка залежить від часу, положення точки і її швидкості. Розглянемо розв’язання другої задачі динаміки в цьому випадку.

Напрямимо координатну вісь (позначимо її через х) вздовж лінії руху (траєкторії) точки. Деяку точку О, розміщену на лінії руху точки, візьмемо за початок відліку координати х матеріальної точки. Зобразимо матеріальну точку в деякому проміжному (довільному) положенні так, щоб координата точки і напрямок її руху були додатними (рис.1). Прикладемо до точки силу , і напрямимо її в бік до датного напрямку координатної осі, при цьому F=F(t, x, x').

Задамо такі початкові умови руху матеріальної точки:

при .

Складемо диференціальне рівняння руху точки. У проекції на координатну вісь Ox воно запишеться у вигляді:

Інтегруючи це рівняння, дістанемо х як функцію часу t і двох довільних сталих С₁ та С₂, тобто знайдемо загальне рівняння у вигляді:

Наявність у правій частині рівняння довільних сталих інтегрування вказує на те, що під дією даної сили точка може здійснювати не якийсь певний рух, а цілий комплекс рухів. Фізично це означає, що точка, на яку починає діяти сила , буде рухатись по різному в залежності від її початкового положення і початкової швидкості.