Теорема про додавання прискорень 7 страница

Сталі інтегрування визначаються за початковими умовами. Для цього обчислюємо похідну за часом від загального розв’язку:

Підставивши початкові умови в рівняння для визначення x і x', дістанемо два алгебраїчних рівняння:

розв’язуючи які й знайдемо сталі інтегрування.

Накінець, підставивши отримані значення сталих інтегрування в загальний розв’язок, дістанемо рівняння:

яке виражає закон руху матеріальної точки в даному випадку.

У загальному випадку для сили дістати розв’язок диференціального рівняння руху точки в кінцевому вигляді неможливо. Але має місце досить широкий спектр задач динаміки прямолінійного руху точки, для якого розв'язок диференціального рівняння знаходиться в кінцевому вигляді й досить просто. Це, зокрема, коли сила, що діє на точку:

1) стала величина ;

2) залежить тільки від часу ;

3) залежить тільки від координати точки ;

4) залежить тільки від швидкості точки .

Розглянемо тільки перший випадок, коли сила є величиною сталою

Оскільки 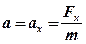і , то . У цьому випадку диференціальне рівняння руху матеріальної точки запишеться у вигляді:

Розв’язання цього рівняння розглядалось в кінематиці (див. лекцію №11). У результаті з урахуванням початкових умов дістали рівняння:

яке виражає закон руху точки в цьому випадку. Цей закон називається законом рівнозмінного прямолінійного руху.

3. Розв’язання другої задачі динаміки при криволінійному русі точки

У випадку криволінійного руху точки друга задача динаміки розв’язується за допомогою диференціальних рівнянь, які ми розглянули на попередній лекції. Якщо задача розв’язується в прямокутних декартових координатах, то початкові умови задаються у вигляді:

при .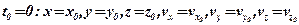

Конкретний хід задачі розглянемо на прикладі руху тіла, кинутого під кутом до горизонтальної площини в однорідному полі тяжіння (рис.2). Вивчимо рух тіла, кинутого з початковою швидкістю , напрямленою під кутом α до горизонтальної площини, розглядаючи його як точку масою m. При цьому опором повітря нехтуємо.

Рис.2

Розмістимо початок координат О в початковому положенні точки. Кут між і віссю Ох буде α.

Зобразимо точку М у довільному положенні. На неї діє тільки сила ваги, проекції якої на координатні осі дорівнюють:

Підставляючи ці значення в диференціальні рівняння руху точки, маємо:

Помноживши обидві частини рівнянь на dt і проінтегрувавши їх, маємо:

Початкові умови в нашій задачі мають вигляд:

при t₀=0: x=0, y=0, z=0, v_x=v₀ cos α, v_y=v₀ sin α, v_z=0.

Задовольняючи початкові умови, маємо:

C₁=v₀cosα, C₂=v₀sinα, C₃=0.

Підставляючи ці значення в рівняння і виражаючи v_x, v_y та v_z через , та 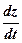, дійдемо рівнянь:

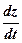=0.

Інтегруючи їх, дістанемо:

Підставлення початкових умов дає С₄=С₅=С₆=0, і в кінцевому вигляді маємо:

z=0.

Із цього виходить, що рух відбувається в площині Oxy. Маючи ці рівняння, можна методами кінематики визначити всі характеристики цього руху: траєкторію точки, горизонтальну дальність польоту, висоту траєкторії, час польоту.

Питання для самоконтролю

1. У чому полягає друга задача динаміки, і в якій послідовності вона розв’язується?

2. Алгоритм розв’язання другої задачі динаміки при прямолінійному русі матеріальної точки.

3. Розв’язання другої задачі динаміки, якщо сила, що діє на точку, є величиною сталою.

4. Алгоритм розв’язання другої задачі динаміки при криволінійному русі точки.

Лекція №28

Тема: “Невільний і відносний рухи точки. Прямолінійні коливання точки ”

План

1.Невільний рух матеріальної точки.

2.Відносний рух матеріальної точки.

3.Вільні коливання точки.

4.Вимушені коливання. Явище резонансу.

1.Невільний рух матеріальної точки

Якщо точка невільна, тобто якщо на неї накладені в’язі, які обмежують рух точки, то при розв’язанні задач динаміки користуються принципом звільнення.

Подумки відкидають в'язі, заміняють їх дію на точку реакціями цих в’язей і розглядають точку як вільну, яка здійснює рух під дією прикладених до неї активних сил та реакцій в’язей.

Тоді диференціальні рівняння руху матеріальної точки запишуться у вигляді:

а) у векторній формі:

де – рівнодійна активних сил, – рівнодійна сил реакцій;

б) у координатній формі:

де F_x, F_y, F_z – алгебраїчні суми проекцій всіх активних сил на координатні осі х, у, z; R_x, R_y, R_z – алгебраїчні суми проекцій всіх сил реакцій на відповідні координатні осі;

в) у натуральній формі:

де F_τ, F_n – алгебраїчні суми проекцій всіх активних сил на дотичну вісь та головну нормаль; R_τ, R_n – алгебраїчні суми проекцій всіх сил реакцій на відповідні осі.

Якщо точка невільна, то перша задача динаміки зводиться до того, щоб, знаючи закон руху точки і активні сили, що діють на неї, визначити реакції накладених на точку в’язей. Друга задача динаміки при невільному русі розкладається на дві й полягає у тому, щоб, знаючи активні сили, що діють на точку, визначити: а) закон руху точки; б) реакцію накладеної в'язі.

2.Відносний рух матеріальної точки

Другий закон динаміки і рівняння, які ми дістали на його основі, справедливі тільки для абсолютного руху точки, тобто руху по відношенню до інерціальної („нерухомої”) системи відліку.

Тепер звернемось до відносного руху точки, тобто руху по відношенню до неінерціальних, які як завгодно рухаються по відношенню до інерціальних, систем відліку.

Розглянемо матеріальну точку М, що рухається під дією прикладених до неї сил , ,..., , які є результатом взаємодії точки з іншими матеріальними тілами. Будемо вивчати рух цієї точки в системі Oxyz (рис.1), які в свою чергу за відомим нам законом рухаються відносно інерціальної системи відліку (нерухомих осей) .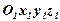

Необхідно знайти залежність між відносним прискоренням точки і силами, які діють на неї. Для абсолютного руху точки основний закон динаміки має вигляд:

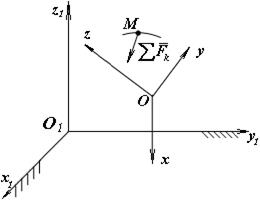
Рис.1

З кінематики відомо, що , де – відносне, переносне і коріолісове прискорення точки. Підставляючи значення в рівняння і вважаючи далі (оскільки ця величина вивчається нами), дістанемо:

Введемо позначення:

Величини мають розмірність сили. Назвемо їх переносною і коріолісовою силами інерції. Тоді попереднє рівняння набуде вигляду:

Це рівняння виражає основний закон динаміки для відносного руху точки.

Звідси висновок: всі рівняння і теореми механіки для відносного руху точки складаються так само, як рівняння для абсолютного руху, якщо при цьому до сил, що діють на точку, додати переносну і коріолісову сили інерції.

Деякі часткові випадки:

1. Якщо рухомі осі рухаються поступально, то (ω=0, де ω – кутова швидкість обертання рухомих осей Oxyz), і закон відносного руху буде мати вигляд:

2. Якщо рухомі осі переміщаються поступально, рівномірно і прямолінійно, то 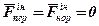, і закон відносного руху буде таким же, як і закон по відношенню до нерухомих осей. Отже, така система відліку буде також інерціальною.

3. Якщо точка по відношенню до рухомих осей знаходиться в спокої, то для неї , тому (). Тоді маємо:

Це рівняння є рівнянням відносної рівноваги (спокою) точки. Із нього виходить, що рівняння рівноваги складаються так само, як рівняння рівноваги в нерухомих осях, якщо при цьому до діючих на точку сил взаємодії з іншими тілами додати переносну силу інерції.

3. Вільні коливання точки

Вивчення механічних коливань є важливим тому, що вони дуже часто зустрічаються в техніці.

Розглянемо точку M, яка рухається прямолінійно під дією однієї тільки поновлюючої сили , напрямленої до нерухомого центра O і пропорційної відстані від його центра. Проекція сили на вісь Ox буде (рис.2):

Сила намагається повернути точку в положення рівноваги О, де F=0, тому і назва „поновлююча” сила. Прикладом такої сили є сила пружності.

Знайдемо закон руху точки M. Складемо диференціальне рівняння руху в проекції на вісь х, дістанемо:

або

Розділивши обидві частини рівняння на m і ввівши позначення

дійдемо результату:

Це рівняння є диференціальним рівнянням вільних коливань при відсутності опору.

Розв'язок цього лінійного однорідного диференціального рівняння другого порядку шукають у вигляді: . Покладаючи в рівнянні , для визначення n дістанемо характеристичне рівняння . Як відомо з теорії диференціальних рівнянь, загальний розв'язок цього рівняння має вигляд:

де С₁ і С₂ – сталі інтегрування.

Якщо замість сталих С₁ і С₂ ввести сталі А і α, такі, що , , то дістанемо:

x=A(sin kt cos α+cos kt sin α)

або

Це другий вигляд розв’язання диференціального рівняння, де сталі інтегрування А і α. Ним зручніше користуватись для загальних досліджень.

Швидкість точки в цьому русі:

Коливання, здійснювані за цим законом, називаються гармонійними коливаннями точки.

Всім характеристикам цього руху можна дати наочну кінематичну інтерпретацію.

Розглянемо точку В, яка рухається рівномірно по колу радіуса А із положення В₀, яке визначається кутом (рис.3). Нехай стала кутова швидкість обертання радіуса дорівнює k. Тоді в довільний момент часу t кут , і легко бачити, що проекція M точки B на діаметр, перпендикулярний DE рухається за законом x=Asin (kt+α), де x=OM, тобто здійснює гармонійні коливання.

Величина A, яка дорівнює найбільшому відхиленню точки M від центра О, називається амплітудою коливань. Величина φ=kt+α називається фазою коливань. Фаза φ на відміну від координати x визначає не тільки положення точки в даний момент часу, а й напрямок її подальшого руху; наприклад, із положення M при фазі φ точка рухається вправо, а при фазі (π – φ) – вліво. Фази, які відрізняються на 2π, вважаються однаковими. Величина α визначає фазу початку коливань (початкова фаза).

Величина k, яка збігається з кутовою швидкістю обертання радіуса OB, називається круговою частотою коливань.

Проміжок часу T (або τ), за який точка здійснює одне повне коливання, називається періодом коливань. По проходженні періоду фаза змінюється на 2π. Отже, повинно бути kТ=2π, звідки період:

Величина 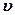, обернена періоду, яка визначає кількість коливань за 1с, називається частотою коливань:

Величина k відрізняється від 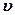на сталий множник 2π. Далі ми будемо частотою коливань називати величину k.

Визначимо сталі інтегрування А і α за початковими умовами: вважаємо, при t₀=0: x=x₀, v_x=v₀, тоді . Звідси склавши почленно квадрати цих рівнянь, а потім розділивши їх почленно одне на інше, знайдемо:

Вплив сталої сили на вільні коливання точки. Нехай на точку М, крім поновлюючої сили , напрямленої до центра О (чисельно F=c OM), діє стала за модулем сила (рис.4).

Рис.4

У цьому випадку положенням рівноваги точки М, де сила зрівноважиться з силою , буде точка О₁, яка розміщена на відстані OO₁=λ_cт від точки О. Ця відстань визначається рівністю сλ_cт=Р або

Величину λ_cт назвемо статичним відхиленням.

Отже, стала сила не змінює характер коливань, лише зміщає центр коливань у бік дії сили на величину статичного відхилення λ_cт.

Виразимо період коливань через λ_cт. Оскільки , тоді:

4. Вимушені коливання. Явище резонансу

Розглянемо випадок коливань, які виникають тоді, коли на точку, крім поновлюючої сили , діє ще сила , яка змінюється з часом і проекція якої на вісь х дорівнює:

Q_x=Q₀sin pt.

Ця сила називається збуджуючою, а коливання, що здійснюються під дією такої сили, називаються вимушеними. Величина р називається частотою збуджуючої сили.

Розглянемо рух точки, на яку, крім поновлюючої сили , діє тільки збуджуюча сила . Диференціальне рівняння руху в цьому випадку буде:

Розділимо обидві частини рівняння на m і покладемо, що:

,

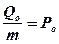де P₀ має розмірність прискорення.

Тоді диференціальне рівняння руху має вигляд:

Це рівняння є диференціальним рівнянням вимушених коливань точки при відсутності опору.

Загальний розв'язок рівняння має вигляд:

або

де А і α – сталі інтегрування, які визначаються за початковими умовами.

Цей розв'язок показує, що коливання в цьому випадку складаються з: 1) коливань із амплітудою А (яка залежить від початкових умов) і частотою k, які називаються власними коливаннями; 2) коливань із амплітудою B (яка не залежить від початкових умов) і частотою p, які називаються вимушеними коливаннями.

Резонанс. У випадку коли p=k, тобто частота збуджуючої сили дорівнює частоті власних коливань, має місце явище, яке називається резонансом. Можна довести, що розмахи вимушених коливань при резонансі будуть з часом необмежено зростати (рис. 5).

Питання для самоконтролю

1.Записати диференціальні рівняння невільного руху матеріальної точки у трьох формах: векторній, координатній та натуральній.

2.Вивести рівняння, що виражає основний закон динаміки для відносного руху матеріальної точки.

3.Охарактеризувати часткові випадки відносного руху точки.

4.Вивести диференціальне рівняння вільних коливань точки. Його загальні розв’язки в двох виглядах.

5.Дати кінематичну інтерпретацію всім характеристикам вільних коливань точки.

6.Що називається амплітудою коливань, фазою, початковою фазою, круговою частотою, частотою та періодом коливань?

7.Як визначаються сталі інтегрування А та α?

8.Як впливає стала сила на характер вільних коливань точки?

9.Коли виникають вимушені коливання матеріальної точки?

10. Записати диференціальне рівняння вимушених коливань точки та його загальний розв’язок.

11. Дати пояснення явищу резонансу.

Лекція №29

Тема: “Вступ в динаміку системи”

План

1.Механічна система. Класифікація сил, що діють на систему.