 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Дифференциал
|
|
Пусть 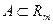 ,
, 

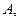
 . Предположим, что функция
. Предположим, что функция  дифференцируема в точке
дифференцируема в точке  .
.
Определение 1. Дифференциал (или первый дифференциал) функции  в точке
в точке  есть функция переменных
есть функция переменных 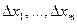 , обозначаемая символом
, обозначаемая символом 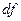 и определяемая равенством
и определяемая равенством
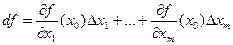 .
.
Дифференциалом независимой переменной 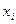 будем называть приращение независимой переменной:
будем называть приращение независимой переменной: 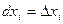 . Тогда
. Тогда
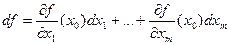 . (1)
. (1)
Теорема 1. Пусть 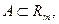
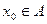 ,
,  и
и  - функции, заданные на
- функции, заданные на 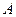 и дифференцируемые в точке
и дифференцируемые в точке  . Тогда:
. Тогда:
1) 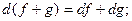
2) 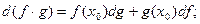
3) если 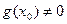 , то
, то 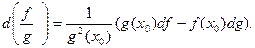
Дата публикования: 2015-09-18; Прочитано: 176 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
