Непрерывность и алгебраические операции над функциями

Теорема 1. Пусть 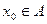, и - функции, заданные на 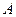и непрерывные в точке . Тогда:

1) непрерывна в точке ;

2) 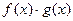непрерывна в точке ;

3) 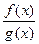при условии, что 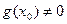, также непрерывна в точке .

6) Непрерывность сложной функции.

Пусть 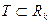, , 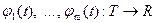, 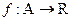. Тогда мы можем на множестве рассматривать функцию переменных , определенную равенством

= .

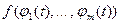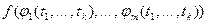Эту функцию называют сложной функцией.

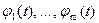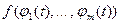Теорема 1. Если функции непрерывны в точке , а функция непрерывна в точке , то сложная функция непрерывна в точке .

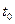7) Определение частной производной.

Пусть 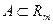, , -внутренняя точка множества 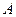. Если приращение 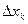независимого переменного достаточно мало, то . При переходе от точки к точке

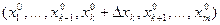функция получает приращение

= - ,

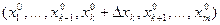которое называется частным приращением функции в точке , отвечающим приращению 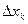аргумента .

Определение 1. Частной производной функции по аргументу в точке называют

, если он существует и конечен.

Обозначение: , .

При фиксированных значениях всех аргументов, кроме , функция становится функцией одного переменного. Производная этой функции одного переменного и есть частная производная функции по переменной . Поэтому вычисление частных производных производится по тем же правилам, что и вычисление производных функций одной переменной.

Физический смысл частной производной - это скорость изменения функции в точке вдоль оси - ов.