 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Локальный экстремум
|
|
Определение 1. Пусть 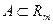 ,
, 

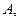
 . Говорят, что функция
. Говорят, что функция  имеет в точке
имеет в точке  локальный максимум, если найдется
локальный максимум, если найдется 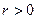 такое, что:
такое, что:
1) 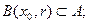
2) 
Локальный максимум называется строгим, если  найдется
найдется 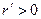 такое, что
такое, что


Аналогично определяется понятие локального минимума и строгого локального минимума.
Точки локального минимума и локального максимума называются точками локального экстремума.
Теорема 1 (необходимое условие экстремума). Пусть 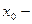 точка локального экстремума. Если существует
точка локального экстремума. Если существует  , то
, то 
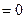 .
.
Определение 2. Точка  , внутренняя для множества
, внутренняя для множества 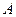 , называется критической (стационарной) точкой функции
, называется критической (стационарной) точкой функции  , если в ней существуют и равны нулю все частные производные первого порядка.
, если в ней существуют и равны нулю все частные производные первого порядка.
Каждая точка локального экстремума является критической. Обратное неверно.
Пример 1. Пусть 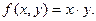 Тогда точка
Тогда точка 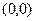 - критическая точка функции
- критическая точка функции  , но не точка локального экстремума этой функции.
, но не точка локального экстремума этой функции.
Достаточное условие локального экстремума.
Определение3. Матрица 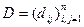 размера
размера  называется положительно определенной, если
называется положительно определенной, если  произведение
произведение 
Теорема 2 (Критерий Сильвестра положительной определенности матрицы).
Пусть
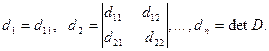
Матрица  положительно определена тогда и только тогда, когда
положительно определена тогда и только тогда, когда 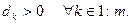
Определение 4. Матрица 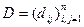 размера
размера  называется отрицательно определенной, если
называется отрицательно определенной, если  произведение
произведение 
Очевидно, матрица  отрицательно определена тогда и только тогда, когда матрица
отрицательно определена тогда и только тогда, когда матрица 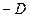 положительно определена.
положительно определена.
Теорема 3 (Критерий отрицательной определенности матрицы).
Матрица  отрицательно определена тогда и только тогда, когда
отрицательно определена тогда и только тогда, когда
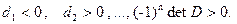
Определение5. Матрица  называется неопределенной, если найдутся
называется неопределенной, если найдутся 
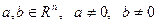 такие, что
такие, что 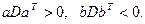
Теорема 4. Пусть  - открытое множество,
- открытое множество, 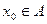 ,
,  . Допустим, что функция
. Допустим, что функция  в каждой точке множества
в каждой точке множества 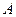 имеет все частные производные до второго порядка включительно и эти производные непрерывны. Пусть
имеет все частные производные до второго порядка включительно и эти производные непрерывны. Пусть  - критическая точка функции
- критическая точка функции  . Тогда:
. Тогда:
1) если матрица  положительно определена, то
положительно определена, то  есть точка строгого локального минимума;
есть точка строгого локального минимума;
2) если матрица  отрицательно определена, то
отрицательно определена, то  есть точка строгого локального максимума;
есть точка строгого локального максимума;
3) если матрица  является неопределенной, то
является неопределенной, то  не является точкой локального экстремума.
не является точкой локального экстремума.
Случай 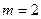 .
.
Рассмотрим функцию двух переменных, для которой  - критическая точка. Матрица вторых производных имеет вид
- критическая точка. Матрица вторых производных имеет вид
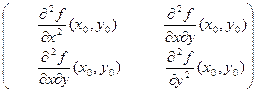 .
.
Положим

 ,
, 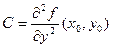 .
.
Логически возможны три случая:
Случай 1: 
Случай 2: 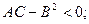
Случай 3: 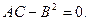
В первом случае 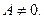 Если
Если
 ,
,
то  - точка строгого локального минимума. Если
- точка строгого локального минимума. Если
 ,
,
то  - точка строгого локального максимума.
- точка строгого локального максимума.
Во втором случае дискриминант квадратного трехчлена 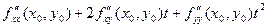
положителен. Следовательно, найдутся  и
и  такие, что
такие, что

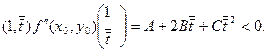
Значит матрица  является неопределенной, и локального экстремума в точке
является неопределенной, и локального экстремума в точке  нет.
нет.
В третьем случае в точке  экстремум может как быть, так и не быть.
экстремум может как быть, так и не быть.
Пример 2. Пусть 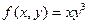 . Тогда
. Тогда 
 Следовательно точка
Следовательно точка 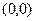 критическая. Очевидно, у функции
критическая. Очевидно, у функции  в точке
в точке 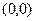 экстремума нет.
экстремума нет.
Так как 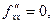

 то
то  в точке
в точке 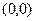 , и тем самым
, и тем самым
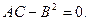
Пример 3. Пусть 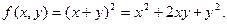 Очевидно, у функции
Очевидно, у функции  в точке
в точке 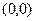 экстремум,
экстремум, 



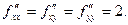
 Поэтому
Поэтому
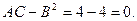
Дата публикования: 2015-09-18; Прочитано: 249 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
