 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Касательная плоскость и нормаль к поверхности
|
|
 |
Рассмотрим непрерывную функцию
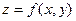 двух переменных. Ее график, т.е. множество точек
двух переменных. Ее график, т.е. множество точек 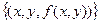 есть некоторая поверхность
есть некоторая поверхность 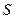 в пространстве
в пространстве 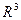 . Пусть плоскость
. Пусть плоскость 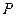 проходит через точку
проходит через точку  поверхности
поверхности 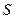 ,
, 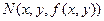 – произвольная точка на поверхности
– произвольная точка на поверхности 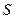 ,
,  – основание перпендикуляра, проведенного из точки
– основание перпендикуляра, проведенного из точки 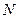 к плоскости
к плоскости 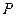 .
.
Определение 1. Плоскость 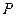 , проходящая через точку
, проходящая через точку  поверхности
поверхности 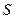 , называется касательной плоскостью к поверхности
, называется касательной плоскостью к поверхности 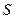 в этой точке, если
в этой точке, если 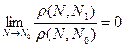 , т.е. расстояние между точками
, т.е. расстояние между точками 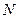 и
и  есть бесконечно малая более высокого порядка, чем расстояние между точками
есть бесконечно малая более высокого порядка, чем расстояние между точками 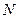 и
и  .
.
Теорема 1. Если функция  дифференцируема в точке
дифференцируема в точке  , то в точке
, то в точке  существует касательная плоскость к поверхности
существует касательная плоскость к поверхности 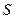 . При этом уравнение касательной плоскости имеет вид
. При этом уравнение касательной плоскости имеет вид
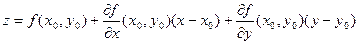 .
.
Дата публикования: 2015-09-18; Прочитано: 250 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
