Производные старших порядков

Предположим, что функция 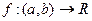дифференцируема на интервале , т.е. " x Î(a, b) 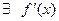.Определим на интервале функцию g равенством: g (x)= .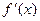

Определение 1. Если в точке 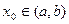существует производная функции g, то эта производная называется производной второго порядка функции 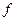в точке и обозначается одним из символов:

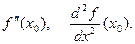
Если производная порядка n 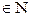определена (ее обозначение 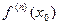или 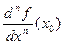), и для любого 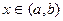существует 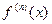, то производная в точке 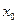порядка (n +1) определяется как 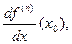если последняя существует.

Пример 1. Пусть 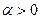. Тогда для и

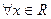
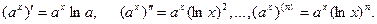
В частности,

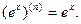
Пример 2. Для и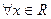

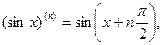
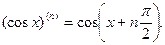
Пример 3. Пусть aÎ 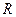. Для и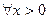

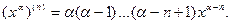
В частности, для и ,  

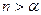
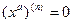" x Î .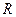

Пример 4. Для и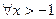 

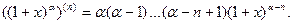
Пример 5. Для и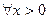 

Далее полагаем

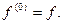
Теорема 1. Предположим, что функции f и g имеют на (a, b) производные порядка n. Тогда:

1)

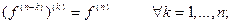
2) ;

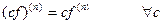3)

4) 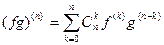(Формула Лейбница).