 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Примеры вычисления производных
|
|
1) 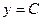 .
.
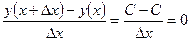 , поэтому у¢ =0.
, поэтому у¢ =0.
2) у=хп, где п – натуральное число.
n =1: у ¢= х ¢=1, т.к. 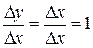 .
.
п =2: у = х × х;
у ¢=(х)¢× х +(х)¢× х =2 х.
 =3: у =(х 2)× х;
=3: у =(х 2)× х;
у ¢=(х 2)¢× х +(х)¢× х 2 =2 х 2 +х 2=3 х 2.
Во всех рассмотренных случаях (хп)¢= пхп-1. Для произвольного натурального п также (хп)¢= пхп-1.
3) 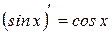 .
.
Действительно,
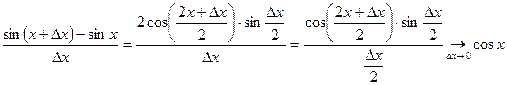 .
.
4) 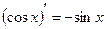 .
.
Действительно,
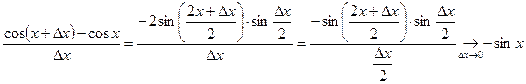 .
.
5) 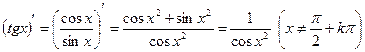 .
.
6) 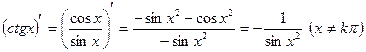 .
.
7) 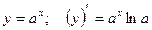 .
.
Действительно,
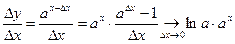 .
.
В частности, 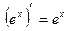 .
.
8) 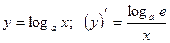 .
.
Действительно,
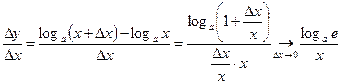 .
.
В частности, 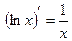 .
.
9) 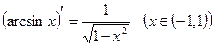 .
.
Действительно, пусть  . Тогда
. Тогда 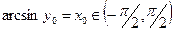 ,
, 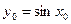 ,
, 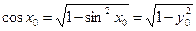 . По теореме о производной обратной функции
. По теореме о производной обратной функции
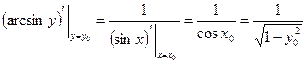 .
.
Таким образом,
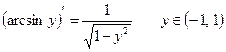 .
.
Традиционно аргумент функции обозначается через х. Переходя к традиционному обозначению аргумента, получаем
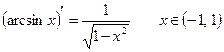 .
.
10) 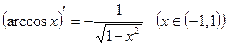 .
.
Действительно, пусть 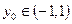 . Тогда
. Тогда 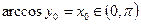 ,
,  ,
, 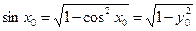 . По теореме о производной обратной функции
. По теореме о производной обратной функции
 .
.
Таким образом,
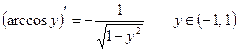 .
.
Переходя к традиционному обозначению аргумента, получаем
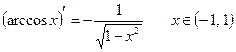 .
.
11) 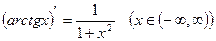 .
.
Действительно, пусть  . Тогда
. Тогда 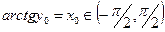 ,
, 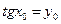 ,
, 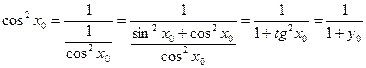 . По теореме о производной обратной функции
. По теореме о производной обратной функции
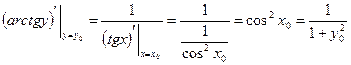 .
.
Таким образом,
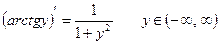 .
.
Переходя к традиционному обозначению аргумента, получаем
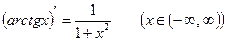 .
.
12) 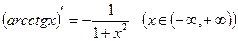 .
.
Действительно, пусть 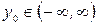 . Тогда
. Тогда 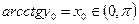 ,
, 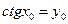 ,
, 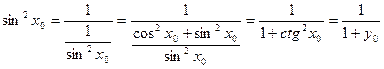 . По теореме о производной обратной функции
. По теореме о производной обратной функции
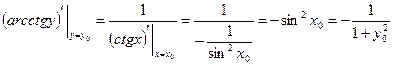 .
.
Таким образом,
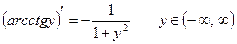 .
.
Переходя к традиционному обозначению аргумента, получаем
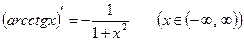 .
.
13) Пусть натуральное число 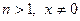 принадлежит области определения функции
принадлежит области определения функции 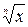 . Тогда
. Тогда 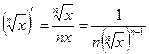 .
.
Действительно, пусть 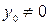 принадлежит области определения функции
принадлежит области определения функции 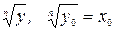 . Тогда
. Тогда 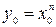 . По теореме о производной обратной функции
. По теореме о производной обратной функции 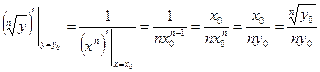 . Таким образом, для
. Таким образом, для 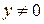 из области определения функции
из области определения функции 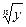 имеем
имеем
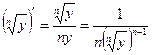 ,
,
или, переходя к традиционному обозначению аргумента,
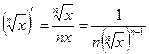 .
.
В частности
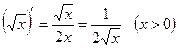 ,
,
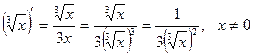 .
.
14) 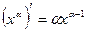 (a – произвольное вещественное число, х >0).
(a – произвольное вещественное число, х >0).
Действительно, согласно определению степенной функции с произвольным вещественным показателем, 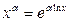 . Применяя теорему о производной сложной функции, получаем
. Применяя теорему о производной сложной функции, получаем
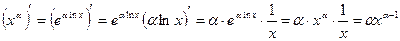 .
.
15) Производные гиперболических функций находятся по формулам:
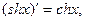
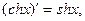
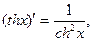
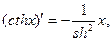
так как 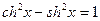 .
.
Дата публикования: 2015-09-18; Прочитано: 306 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
