 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Односторонние производные
|
|
Определение 1. Пусть  . Если существует конечный предел
. Если существует конечный предел
 ,
,
то этот предел называется производной слева функции f в точке х 0 и обозначается символом  .
.
Определение 2. Пусть  . Если существует конечный предел
. Если существует конечный предел
 ,
,
то этот предел называется производной справа функции f в точке х 0 и обозначается символом  .
.
Существуют функции, имеющие в данной точке 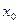 и левую, и правую производные, но не имеющие производной в этой точке. Примером такой функции может служить функция
и левую, и правую производные, но не имеющие производной в этой точке. Примером такой функции может служить функция  Эта функция имеет в точке 0 правую производную, равную 1, левую производную, равную -1, и не имеет производной.
Эта функция имеет в точке 0 правую производную, равную 1, левую производную, равную -1, и не имеет производной.
Теорема 1. Для того чтобы функция 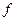 имела в точке
имела в точке 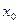 производную, необходимо и достаточно, чтобы:
производную, необходимо и достаточно, чтобы:
1) 
2) 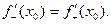
Дата публикования: 2015-09-18; Прочитано: 231 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
