 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Приклад 10
|
|
Вектор 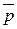 перпендикулярний до векторів
перпендикулярний до векторів  і
і 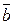 . Довести, що
. Довести, що 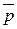 перпендикулярний до будь-якої лінійної комбінації цих векторів.
перпендикулярний до будь-якої лінійної комбінації цих векторів.
Розв’язання: Оскільки  і
і 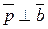 , то
, то  і
і  . Нехай
. Нехай  . Тоді за властивостями 2 і 3
. Тоді за властивостями 2 і 3

Отже,  .
.
 Приклад 11.
Приклад 11.
Довести, що в будь-якому трикутнику має місце співвідношення:
c2=a2+b2-2abcosC, де a,b,c – довжини сторін трикутника (теорема косинусів). Рис.8
Розв’язання: Розглянемо трикутник ABC (рис. 8). Позначимо  ,
,  ,
, 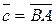 . Тоді
. Тоді  .
. 
 Доведено.
Доведено.
З’ясуємо геометричну суть координат векторів в ортонормованому базисі.
Нехай вектор  - ненульовий вектор заданий в ортонормованому базисі
- ненульовий вектор заданий в ортонормованому базисі  ,
,  ,
,  координатами
координатами  = (а1,а2,а3). Запишемо його розклад по базису:
= (а1,а2,а3). Запишемо його розклад по базису:  . Помноживши обидві частини рівності скалярно на вектори
. Помноживши обидві частини рівності скалярно на вектори  ,
,  ,
,  і враховуючи, що
і враховуючи, що  , а
, а  , маємо
, маємо  ,
,  ,
,  . Позначивши:
. Позначивши:  ,
,  ,
,  , отримаємо
, отримаємо  ;
;  ;
;  . Отже, координати вектора в ортонормованому базисі – це його проекції на координатні вісі.
. Отже, координати вектора в ортонормованому базисі – це його проекції на координатні вісі.
Числа  ,
,  ,
,  називають направляючими косинусами вектора
називають направляючими косинусами вектора  в базисі
в базисі  ,
,  ,
,  .
.
Так як 
 і
і  , то
, то 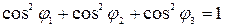 .
.
Отже, сума квадратів направляючих косинусів довільного не нульового вектора дорівнює одиниці.
Відмітимо, що координати одиничного вектора в ортонормованому базисі рівні його направляючим косинусам.
Дата публикования: 2015-09-18; Прочитано: 243 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
