Теорема 7 (Умова колінеарності двох векторів у координатній формі)

Два вектори і 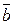колінеарні, тоді і тільки тоді коли їх координати пропорційні.

Доведення:

Нехай вектори і 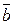в базисі 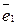, , 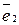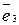мають координати:

=(a₁, a₂, a₃); 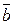= (b₁, b₂, b₃). За умовою теореми || 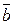. За теоремою 1 існує єдине число α таке, що . Тоді, згідно теореми 6: b₁=αа₁, b₂=αа₂, b₃=αа₃. Отже,

Навпаки, нехай , тоді b₁=αа₁, b₂=αа₂, b₃=αа₃. Розглянемо розклад вектора 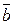по базису:

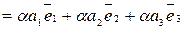
, тобто за теоремою 1 вектори і 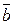колінеарні.