 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Наслідок 10
|
|
Косинус кута α між ненульовими векторами  =(а1,а2,а3) і
=(а1,а2,а3) і 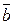 =(b1,b2,b3), заданими в ортонормованому базисі, визначається формулою:
=(b1,b2,b3), заданими в ортонормованому базисі, визначається формулою:
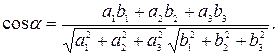
Властивості скалярного добутку:
1.  ·
· 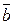 =
= 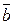 ·
·  (комутативність).
(комутативність).
2. (α  )·
)· 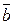 = α (
= α ( ·
· 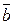 ) (скалярний множник можна виносити за знак скалярного добутку).
) (скалярний множник можна виносити за знак скалярного добутку).
3. 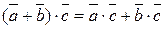 (дистрибутивність).
(дистрибутивність).
Доведення.
1. Властивість випливає з означення скалярного добутку.
2. Нехай в ортонормованому базисі вектори  і
і 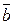 мають координати
мають координати  =(а1,а2,а3) і
=(а1,а2,а3) і 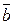 =(b1,b2,b3). Тоді за наслідком 8 вектор
=(b1,b2,b3). Тоді за наслідком 8 вектор 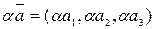 і за теоремою 8
і за теоремою 8 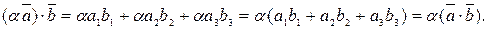
3. Нехай в ортонормованому базисі вектори  ,
, 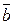 і
і 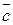 мають координати
мають координати  =(а1,а2,а3),
=(а1,а2,а3), 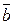 =(b1 b2,b3),
=(b1 b2,b3), 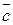 =(c1,c2,c3). За наслідком 6 вектор
=(c1,c2,c3). За наслідком 6 вектор  +
+ 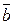 = (a1+b1, a2+b2, a3+b3) і (
= (a1+b1, a2+b2, a3+b3) і (  +
+ 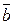 ) ·
) · 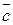 = (a1+b1)c1+(a2+b2)c2+(a3+b3)c3 =
= (a1+b1)c1+(a2+b2)c2+(a3+b3)c3 =
= (a1c1+a2c2+a3c3)+(b1c1+b2c2+b3c3) =  ·
· 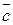 +
+ 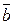 ·
· 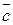 .
.
Дата публикования: 2015-09-18; Прочитано: 204 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
