Сведение кратного интеграла к повторному. Теорема Фубини

Th.: Теорема Фубини.

Если: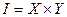

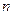- -мерный интервал

- -мерный интервал

То:

Док-во:

Строим разбиение интервалов , выбираем отмеченные точки .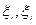

для почти всех

для почти всех

Если этой функции не существует, то можно выбрать любое значение из промежутка между верхней и нижней суммой.

Следствие 1:

почти для всех

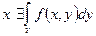
Следствие 2:

Следствие 3:

Если:

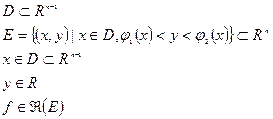
То:

Док-во:

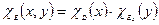
Следствие 4:

Если: в условиях Следствия 3 множество измеримо по Жордану, а функции непрерывны,

То: граница множества 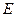имеет меру ноль, множество 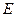измеримо по Жордану: