Лебегова мера ноль

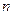Опр.: Будем говорить, что множество имеет -мерную меру ноль в смысле Лебега, если не более чем счётная система интервалов .

1) Точка является множеством меры ноль.

2) Объединение конечного, либо счётного числа множеств меры ноль есть множество меры ноль.

3) Подмножество множества меры ноль – множество меры ноль.

4) Невырожденный 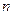-мерный промежуток не является множеством меры ноль.

Опр.: Будем говорить, что некоторое свойство выполняется почти всюду, если оно выполняется всюду, кроме быть может множества меры ноль.

Утв.: График непрерывной функции имеет 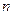-мерную меру ноль.

Если:

То:

Док-во:

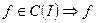равномерно непрерывна на

Строим разбиение . Отмечаем точки разбиения .

Строим промежуток

.

Следствие:

Если:

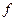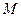То: график на имеет 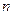-мерную меру ноль.(Т.к. )

Замечание:

1. Если в определении меры ноль заменить замкнутые промежутки открытыми, то определение останется эквивалентным.
2. Если - компакт, то в определении можно заменить счётную систему конечной.

Th.: Критерий Лебега интегрируемости функции по Риману.