Векторная функция скалярного аргумента

Опр.:

1. - векторная функция скалярного аргумента

2.

3. - кусочно гладкая, когда - кусочно гладкие

4. Отображение - путь. Образ при отображении - носитель пути (параметризованная кривая)

Свойства предела.

1.

2.

Свойства производной

Опр.: - скорость

1.

2. Если:

- скалярная функция, - вукторная,

То:

Лемма.

Если: - дифференцируема,

То: .

Док-во:

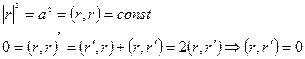
Следствие:

Если точка движется по сфере, то скорость направлена по касательной к сфере.

Опр.: 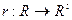- путь

Опр.:

1. Если - биекция, 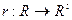, , то - кривая (носитель пути).
2. Гладкость кривой определяется гладкостью функций .
3. Кривая – одномерное многообразие в

Опр.:

Если:

, то касательная в точке имеет вид:

или

- в векторной форме

или

или