Зв'язок між координатами точки в різних системах координат у тривимірному просторі

Розглянемо в просторі дві довільні системи координат, перша з яких задається точкою 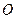та базисом , а друга – точкою та базисом . Нехай координатами деякої точки 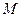відносно першої системи є числа та , а відносно другої – та . Знайдемо зв'язок між цими числами. Нехай точка має координати , а вектори 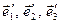виражаються через базис у вигляді рівностей:

,

,

.

Матрицю називають матрицею переходу від базису до базису . Зауважимо, що , інакше її стовпці були б лінійно залежними, що суперечить лінійній незалежності векторів 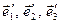, як базисних.

Із векторної рівності 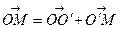аналогічно, як у випадку площини, дістаємо

,

звідки, прирівнюючи коефіцієнти біля базисних векторів, отримуємо

(2)

Співвідношення (2) виражають зв'язок між координатами точки в різних просторових системах координат. При із формул (2) дістаємо

Одержані співвідношення називають формулами паралельного перенесення в просторі.