Приклади. Задача 1. Задано прямокутник

Задача 1. Задано прямокутник . Довести, що для довільної точки 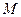виконується рівність .

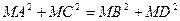Доведення. Введемо прямокутну систему координат наступним чином: точку виберемо початком координат, пряму – віссю , а пряму – віссю . Нехай . Тепер кожна точка матиме свої координати: , . Скориставшись формулою відстані між двома точками, дістаємо

,

.

З рівності правих частини отримуємо необхідне співвідношення.

Задача 2. У трикутній піраміді вершини сполучено з центрами протилежних граней. Довести, що утворені відрізки перетинаються в одній точці та діляться нею у відношенні 3:1, рахуючи від вершини.

Розв’язання. По-перше, зауважимо, що дану задачу ми уже розглядали в лекції 2, розв’язуючи її векторним методом. Тепер ми використаємо координатний метод. Введемо у розгляд загальну афінну систему координат, вибравши точку початком координат та базис . Тоді вершини піраміди матимуть наступні координати:

.

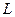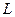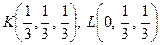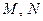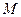Нехай точки та – точки перетину медіан трикутників та відповідно. Координати точок та знайдемо, як середні арифметичні відповідних координат вершин трикутників: . Нехай точки ділять відрізки та у відношенні 3:1, рахуючи від точок та відповідно. Скориставшись формулами поділу відрізка у даному відношенні при , дістаємо , . Оскільки точки та співпадають, то твердження доведено.