Скалярний добуток двох векторів. Властивості. Застосування

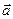Розглянемо на площині або в просторі два довільні вектори та 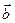. Нехай .

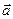Кутом між векторами та 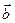назвемо кут між променями та . Причому з двох кутів, які при цьому утворюються, вибиратимемо той, який не перевищує 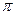, тобто 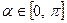(рис. 1).

Означення 1.Скалярним добутком векторів 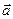та 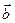називають число

.

Позначатимемо скалярний добуток символом 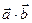або . Отже, згідно з означенням,

= .

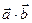Розглянемо деякі властивості введеної операції.

Властивість 1. (комутативність скалярного множення).

Властивість 2. .

Властивість 3. . Звідси (вираз називають скалярним квадратом вектора ).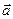

Доведення властивостей 1 – 3 безпосередньо випливають із означення скалярного добутку.

Означення 2. Два вектори домовимось називати ортогональними та записувати 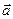^ 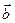, якщо вони утворюють кут .

Властивість 4. Два ненульові вектори ортогональні тоді і тільки тоді, коли їхній скалярний добуток рівний нулю.

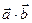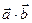Для доведення скористаємось рівністю = . Якщо , то , тому . Якщо , то і, отже, =0.

Властивість 5. Якщо 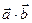>0, то кут між векторами 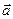та 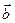гострий. Якщо 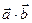<0, то кут між векторами тупий.

Доведення даної властивості випливає із означення скалярного добутку та властивостей функції . Вірне також обернене твердження.

Означення 3. Число називають проекцією вектора 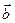на вектор 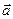та позначають . Тобто = (рис. 2).

Властивість 6. = .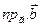

Доведення властивості 6 випливає із означення скалярного добутку.

Знайдемо співвідношення для обчислення скалярного добутку у випадку, коли вектори та задані своїми координатами. Розглянемо вектори . Вважаючи їх не колінеарними, розглянемо трикутник такий, що . За теоремою косинусів

, (*)

де 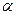– кут між сторонами та . Оскільки

і ,

то, використавши формулу, яка виражає довжину вектора через його координати, з рівності (*) дістаємо

.

Звідси

. (1)

Покажемо, що співвідношення (1) вірне також у випадку колінеарності векторів.

Нехай вектори та колінеарні та виконується векторна рівність . Запишемо її у координатній формі у виді рівностей , , .

При кут між векторами та рівний 0, тому

= + + =

.

При кут між векторами та рівний 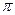, тому

= + + =

.

Таким чином, рівність (1) виконується для довільних векторів та . Використаємо рівність (1) для доведення інших властивостей скалярного добутку.

Властивість 7. (дистрибутивність скалярного множення).

Для доведення властивості 7 припустимо, що вектор 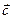задано у виді . Тоді . Із рівності (1) дістаємо

.

Властивість 8. Для довільного числового множника 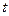виконуються співвідношення .

Доведення даної властивості пропонуємо виконати самостійно.

Наступні властивості фактично повторюють деякі із попередніх, тільки подаються у координатній формі. Ми пропонуємо їх без доведення.

Властивість 9. Вектори та ортогональні тоді і тільки тоді, коли виконується рівність

.

Якщо 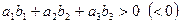, то кут між векторами та гострий (тупий).

Вірне також обернене твердження.

Кут між векторами та можна обчислити, користуючись співвідношенням

. (2)

Властивість 10. Проекцію вектора на вектор можна обчислювати за формулою

. (3)

Зауважимо, що розглянуті властивості та одержані співвідношення мають місце також у випадку, коли кожний із векторів задається двома координатами. Зокрема, якщо задані вектори , то

, , _.

Розглянемо приклади задач, при розв’язуванні яких використовується операція скалярного множення.

Задача 1. У прямокутному трикутнику з катетами та обчислити кут між медіаною, проведеною до гіпотенузи, та бісектрисою прямого кута.

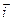Розв’язання. Нехай у прямокутному трикутнику – медіана, проведена до гіпотенузи. Зафіксуємо ортонормований базис , вибравши вектор на промені та вектор на промені . Тоді, оскільки , то . Виберемо один із векторів, які задають напрям бісектриси прямого кута, наприклад, вектор . Скориставшись формулою (1), дістаємо

.

Відповідь. .

Задача 2. Знайти ортогональну проекцію відрізка з кінцями у точках на пряму, що проходить через точки .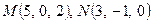

Розв’язання. Розглянемо вектори та і позначимо довжину шуканої проекції через 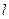. Скориставшись рівністю (3), дістаємо

.

Відповідь. .

Задача 3. Обчислити кут між мимобіжними діагоналлю куба та діагоналлю його бічної грані.

Розв’язання. Нехай – заданий куб. Знайдемо кут між його діагоналлю та діагоналлю бічної грані . Для цього введемо в розгляд прямокутну декартову систему координат, вибравши точку початком координат, а промені вибравши за додатні напрямки осей відповідно та . Нехай ребро куба дорівнює 1. Тоді дістаємо , , , , звідки . Якщо шуканий кут позначити через 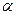, то

.

Відповідь. .

Задача 4. (Теорема Стюарта). Сторони трикутника рівні та . Обчислити довжину відрізка, який сполучає вершину трикутника із точкою, вибраною на стороні , знаючи, що ця точка ділить сторону на відрізки з довжинами та .

Розв’язання. Нехай у трикутнику , , 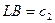, 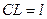– шуканий відрізок (рис. 3). Очевидно, що

.

Тоді

, ,

звідки

, .

Помноживши першу з одержаних рівностей на , а другу – на та додавши одержані співвідношення, дістаємо

,

оскільки = , як сума двох векторів із однаковими довжинами та протилежними напрямками. Рівність

виражає зміст теореми Стюарта та дає відповідь на поставлену задачу.