Поділ відрізка у даному відношенні

Нехай на прямій 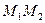вибрана точка 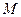, яка ділить відрізок 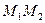у деякому відомому відношенні 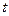. Розглянемо задачу, як, знаючи координати заданих точок та число 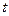, обчислити координати точки .

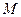Означення. Кажуть, що точка 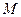ділить відрізок 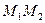у відношенні 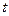, якщо виконується рівність

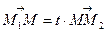. (1)

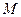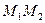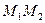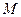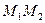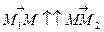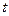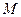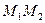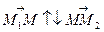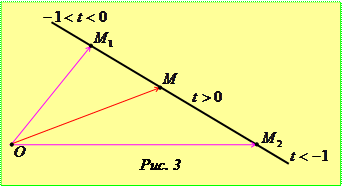
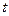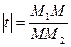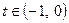
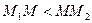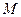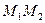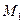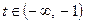
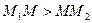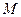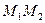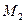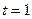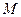Зауважимо, що точка не обов’язково повинна належати відрізку . Вона може лежати на прямій і поза цим відрізком. Очевидно, що якщо точка належить відрізку , то і число >0. Якщо точка лежить поза відрізком , то , тому <0. Вірні також і обернені твердження. Оскільки , то при і точка лежить на прямій поза точкою . При , тому точка лежить на прямій поза точкою (рис. 3). При точка є серединою відрізка 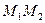. Пр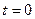и точки 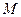та 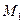співпадають. Випадок 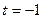неможливий, оскільки тоді з рівності (1) випливає, що кінці відрізка співпадають.

Нехай задані точки 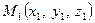та 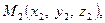а також відношення 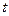, в якому точка ділить відрізок 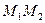. Вважатимемо, що точка 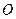є початком координат. Тоді вектори 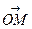, 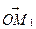та 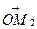мають такі ж координати, як точки 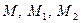. Тому, скориставшись рівністю (1), дістаємо 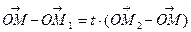, звідки

.

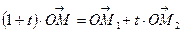Прирівнюючи відповідні координати векторів в обох частинах одержаної рівності, дістаємо

.

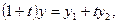
Остаточно,

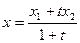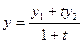, , . (2)

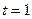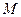Одержані співвідношення називають формулами поділу відрізка у даному відношенні. Зауважимо, що при точка є серединою відрізка 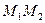. Тому рівності

, ,

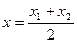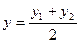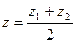
задають координати середини відрізка 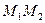. Відмітимо також, що рівності (2) стосуються довільної афінної системи координат, а також, що у двомірному випадку (тобто у випадку, коли точки задаються двома координатами) в одержаних рівностях не розглядають вирази, які містять третю змінну .

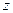Як приклад, знайдемо координати точки перетину медіан трикутника, вершини якого розташовані у точках 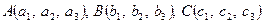. Нехай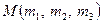 – середина відрізка 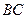, 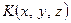– шукана точка. Оскільки

, ,

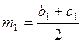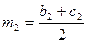
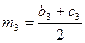то, скориставшись рівностями (2) при 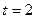(саме у такому відношенні, рахуючи від вершини трикутника, ділить медіани точка їх перетину), дістаємо

, , .

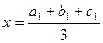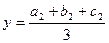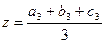Одержаний результат показує, що координати центра маси трикутника є середніми арифметичними відповідних координат вершин трикутника.