Прямокутна декартова системи координат. Відстань між двома точками

Якщо базис ортонормований, то систему координат, яка визначається точкою (початком координат) та базисом 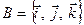називають прямокутною декартовою системою координат у просторі. Нехай у такій системі задані дві точки та . Знайдемо співвідношення, яке виражає відстань між цими точками. Оскільки координати точок співпадають з координатами їхніх радіус-векторів, то , . Тому

.

Знайшовши довжину вектора , яка дорівнює шуканій довжині відрізка , дістаємо формулу відстані між двома точками:

.

У випадку площини, коли система координат визначається точкою (початком координат) та базисом 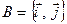, її називають прямокутною декартовою системою координат на площині. Оскільки у цьому випадку точки та вектори визначаються двома координатами: , , то формула відстані між двома точками набуває вигляду

.