 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема Чеви
|
|
Розглянемо довільний трикутник  та візьмемо на його сторонах
та візьмемо на його сторонах  та
та  точки
точки  відповідно. Нехай
відповідно. Нехай  .
.
Вірне наступне твердження.
Теорема (теорема Чеви). Відрізки  та
та  перетинаються в одній точці тоді і тільки тоді, коли виконується рівність
перетинаються в одній точці тоді і тільки тоді, коли виконується рівність 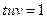 .
.
Доведення. Введемо в розгляд афінну систему координат, вибравши за початок координат точку А та базис  (рис. 4). У цій системі точки матимуть наступні координати:
(рис. 4). У цій системі точки матимуть наступні координати:


 ,
,  ,
,  .
.
 Нехай відрізки
Нехай відрізки  та
та  перетинаються у точці
перетинаються у точці  . Тоді із колінеарності векторів
. Тоді із колінеарності векторів  та
та  , а також векторів
, а також векторів  та
та  дістаємо систему
дістаємо систему  , звідки
, звідки  . Якщо відрізок
. Якщо відрізок  проходить через точку
проходить через точку  , то із колінеарності векторів
, то із колінеарності векторів  та
та 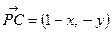
 , дістаємо
, дістаємо  , звідки
, звідки 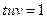 .
.
Із одержаних співвідношень також випливає, що якщо 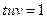 , то вектори
, то вектори  та
та  колінеарні, тобто, що відрізок
колінеарні, тобто, що відрізок  проходить через точку
проходить через точку  перетину двох інших відрізків. Теорема доведена.
перетину двох інших відрізків. Теорема доведена.
Дата публикования: 2015-09-17; Прочитано: 651 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
