Приклади розв’язання задач. Задача 1. У трикутнику на сторонах і

Задача 1. У трикутнику на сторонах і 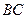вибрано точки та 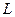так, що , а також проведено відрізки і , які перетинаються у точці . Встановити, у якому відношенні точка ділить дані відрізки.

Розв’язання. Нехай , (рис. 4). Оскільки , то . Виразимо всі вектори в одержаній векторній рівності через 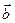та .

,

.

Отже,

.

Оскільки вектори 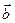та лінійно незалежні, то, прирівнюючи коефіцієнти біля цих векторів в обох частинах рівності, дістаємо систему рівнянь

.

Звідси знаходимо . Отже, .

Відповідь. .

Задача 2. Задано правильний шестикутник . Нехай . Знайти координати векторів та у базисі .

Розв’язання. Нехай 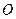– центр кола, описаного навколо заданого шестикутника (рис. 5). Очевидно, що

,

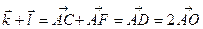а також, що . Тому

,

.

Відповідь. .

Задача 3. Довести, що відрізки, які сполучають вершини трикутної піраміди з центрами протилежних граней, перетинаються в одній точці та діляться нею у відношенні 3:1, рахуючи від вершини.

Розв’язання. Нехай – задана піраміда і , точки та 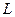– точки перетину медіан відповідно трикутників і , точки 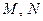належать відрізкам та , причому . Покажемо, що у базисі координати векторів та співпадають. Маємо

,

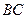де – середина відрізка . Отже, у базисі вектор має координати . Дальше знаходимо

,

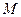тобто . Таким чином, , а це означає, що точки та співпадають.

Задача 4. У трапеції з основами відомо, що . Обчислити координати вектора 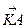у базисі , якщо – точка перетину діагоналей трапеції, (рис. 6).

Розв’язання. Із трикутника знаходимо

.

Оскільки трикутники та подібні, то

.

Звідси . Тому

.

Коефіцієнти біля векторів 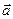та 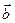дозволяють отримати шукану відповідь.

Відповідь. .